Hans Walser, [20140811]
ggT und kgV, grš§ter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches
Adaptation einer Idee von J. H., A. (Heitzer 2013)
1 Worum geht es?
Die Primfaktorzerlegung von Zahlen wird je in ein Histogramm eingetragen. †berlagerung der Histogramme fźr zwei Zahlen liefert den grš§ten gemeinsamen Teiler und das kleinste gemeinsame Vielfache.
2 Die Vorlage
Wir arbeiten mit einer Transparentfolie mit Formularvordruck gemŠ§ Abbildung 1.
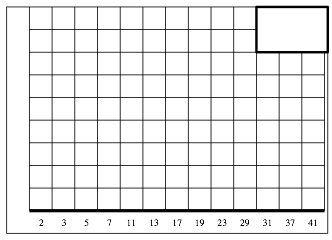
Abb. 1: Transparente Vorlage
3 Profil einer Zahl
Fźr die
natźrliche Zahl 
tragen wir
die Primfaktoren ein gemŠ§ Abbildung 2.
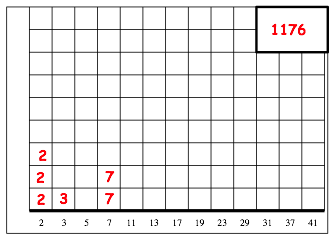
Abb. 2: Eintragen der Primfaktoren
Wir ergŠnzen zu einem Histogramm oder SŠulendiagramm (Abb. 3). Damit haben wir einen Querbezug zur beschreibenden Statistik.
Abb. 3: Histogramm
Die
Potenzschreibeweise 
, welche im Deutschen als ăhochŇ ausgesprochen wird,
kann hier direkt als Hšhe der SŠulen gesehen werden.
4 †berlagerung zweier Profile
Die Abbildungen 4 und 5 zeigen die Profile der Zahlen 84 und 72 in verschiedenen Farben, die Abbildung 5 deren †berlagerung.
Im Unterricht kšnnen sich die Schźlerinnen und Schźler die Profile verschiedener Zahlen gegenseitig ausleihen.
Abb. 4: Profil der Zahl 84
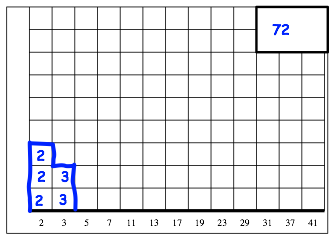
Abb. 5: Profil der Zahl 72
Abb. 6: †berlagerung
5 ggT
Den grš§ten gemeinsamen Teiler finden wir nun dort, wo beide Farben vorkommen (Abb. 7).
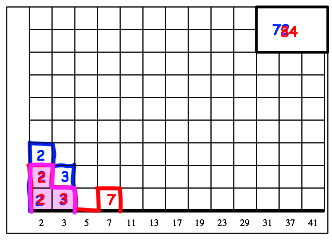
Abb. 7: ggT
Es ist 
.
Wenn wir die Profile der beiden Zahlen 84 und 72 je als Tunnelprofil deuten, hat der grš§te gemeinsame Teiler 12 das Profil des grš§ten Wagens, der gerade noch durch beide Tunnels geht (geschliffen und geschmiert).
6 kgV
Das kleinste gemeinsame Vielfache finden wir dort, wo mindestens eine Farbe vorkommt (Abb. 8).
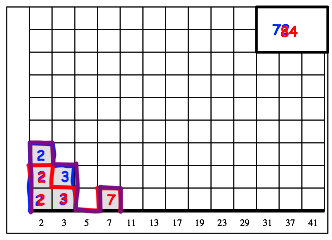
Abb. 8: kgV
Es ist 
.
Das Profil des kleinsten gemeinsamen Vielfaches 504 ist das kleinste Tunnelprofil, durch das die beiden Wagen mit den Profilen der beiden Zahlen 84 und 72 gerade noch hindurchkommen.
Metabemerkung fźr Didaktiker: Beim †bergang vom ggT zum kgV mźssen die Begriffe Tunnel und Wagen vertauscht werden. Max und Moritz sowie der Lehrer LŠmpel merken das auch ohne diesen Hinweis.
7 Umkehrung
Natźrlich dann die Profilvisualisierung auch fźr Umkehrprobleme von der Form
oder 
verwendet werden. Probleme dieser Art sind besonders reizvoll, da sie mehrere Lšsungen, im Falle des ggT sogar unendlich viele Lšsungen zulassen.
Literatur
Heitzer, J. (2013): Lochkarten zur Primfaktorzerlegung. Mathematik lehren, 176, 14-17.