1 Worum geht es?

Reguläre Polygone sind haben gleiche Seiten und gleiche Winkel. Es gibt aber auch gleichseitig-gleichwinklige Polygone, welche nicht regulär sind. Dabei wird der „Winkel“ als Winkel im konvexen Winkelfeld zwischen den beiden anschließenden Seiten verstanden.

Einige Beispiele, ohne Systematik oder Klassifikation.

2 Beispiele

Bei kleinen Eckenzahlen läuft nicht viel. Da gibt es nur die regulären Beispiele.

Abb. 3: Reguläres Dreieck

Abb. 4: Reguläres Viereck

Abb. 5: Reguläres Fünfeck

Abb. 6: Reguläres Sechseck

Abb. 7: Reguläres Siebeneck

Beim Achteck wird es spannend. Neben dem regulären Achteck (Abb. 8a) gibt es auch ein gleichseitig-rechtwinkliges Achteck (Abb. 8b). Allerdings hat es einen Doppelpunkt.

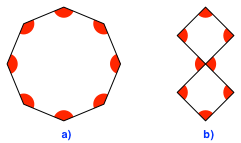
Abb. 8: Achtecke

Auch beim Neuneck gibt es neben dem regulären (Abb. 9a) ein weiteres Beispiel (Abb. 9b). Es hat sogar einen Tripelpunkt. Das reguläre Neuneck kann nicht mit Zirkel und Lineal konstruiert werden, das Beispiel der Abbildung 9b hingegen schon.

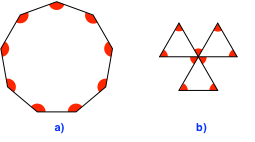
Abb. 9: Neunecke

Beim Zehneck (Abb. 10a) haben wir ein Zusatzbeispiel ohne Mehrfachpunkt (Abb. 10b).

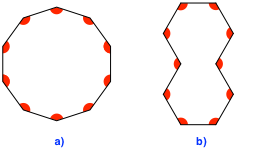
Abb. 10: Zehnecke

Die Zahl elf ist wieder einmal eine schöne Primzahl (Abb. 11).

Abb. 11: Reguläres Elfeck

Gleichseitig-gleichwinklige Zwölfecke gibt es mehrere (Abb. 12a - e).

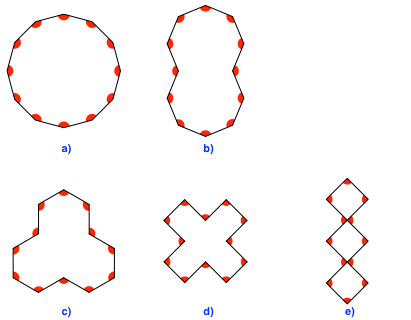
Abb. 12a - e: Zwölfecke

In den Beispielen der Abbildungen 12c – e finden wir mit dem Umkreis den Goldenen Schnitt. In den Abbildungen 12f – h ist er jeweils in der Reihenfolge Minor-Major-Minor eingetragen. Das Beispiel der Abbildung 12f geht auf George Odom (1941-2010) zurück.

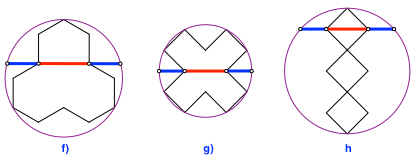
Abb. 12f – h: Der Goldene Schnitt

Abb. 13: Wieder mal eine Primzahl

Bei 14-Ecken gibt es mehrere Möglichkeiten (Abb. 14).

Abb. 14: 14-Ecke

Desgleichen bei 15-Ecken.

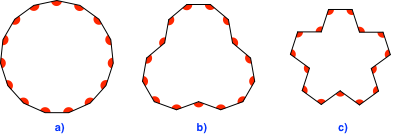
Abb. 15: 15-Ecke

Literatur

Lehmann, Ingmar (2012): Goldener Schnitt, Fibonacci-Zahlen und Goldene Figuren. In: Die Fibonacci-Zahlen und der goldene Schnitt. MU Der Mathematik-Unterricht (58), Heft 1, S. 5-12.

Posamentier, Alfred S. and Lehmann, Ingmar (2012): The Glorious Golden Ratio. Amherst, N.Y., Prometheus Books.

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Weblinks

Hans Walser: Miniaturen: Goldener Schnitt

http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html