Hans Walser, [20131217]

Gleichseitige punktsymmetrische Sechsecke

1     EinfŸhrung

Die Abbildung 1 zeigt das Ÿblich hexagonale Parkett (Bienenwabenmuster).

Abb. 1: Bienenwabenmuster

Die Abbildung 2 zeigt eine Verzerrung dieses Parketts.

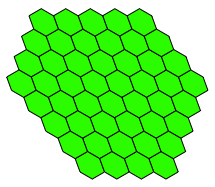
Abb. 2: Verzerrung

 

Das Parkett der Abbildung 3 besteht aus denselben Parkettsteinen wie das bei der Abbildung 2, ist aber auf den ersten Blick weniger regelmŠ§ig.

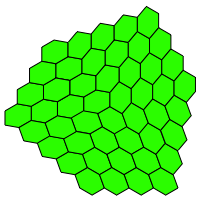
Abb. 3: Andere Anordnung der Parkettsteine

Die Parkette in den Abbildungen 2 und 3 sind topologisch allerdings gleich.

2     AusfŸhrungen zur EinfŸhrung

Bei der Verzerrung vom †bergang vom Parkett der Abbildung 1 zum Parkett der Abbildung 2 handelt es sich nicht um eine affine Abbildung. Die Abbildung 4 zeigt, wie die rote Symmetrieachse zu einer leichten Zickzack-Linie gebrochen wird. Das affine Bild einer geraden Linie mŸsste aber wieder gerade sein.

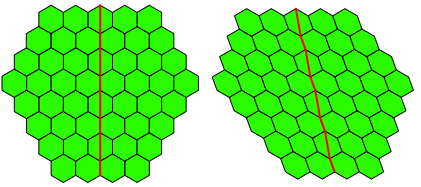
Abb. 4: Bruch der Symmetrieachse. Keine affine Abbildung

 

Das Parkett der Abbildung 3 besteht wohl aus den ãgleichenÒ Parkettsteinen wie das der Abbildung 2. Allerdings mŸssen einige Parkettsteine gewendet werden. In der Abbildung 5 sind diese gewendeten Parkettsteine gelb angegeben. Sie sind spiegelbildlich zu den grŸnen Parkettsteinen.

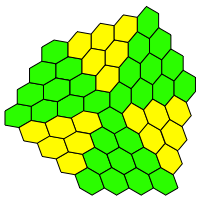
Abb. 5: Die gelben Parkettsteine sind spiegelbildlich zu den grŸnen

Wir sehen nun, dass das Parkett der Abbildungen 3 beziehungsweise 5 eine dreistrahlige Rotationssymmetrie aufweist. DemgegenŸber weist das Parkett der Abbildung 2 eine durchgehende Translationssymmetrie auf.

3     Gleichseitige punktsymmetrische Sechsecke

Ein gleichseitiges punktsymmetrisches Sechseck (Abb. 6) ist (bei gegebener SeitenlŠnge) durch 2 Winkel bestimmt.

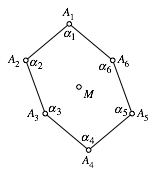
Abb. 6: Gleichseitig punktsymmetrisches Sechseck

Bei Vorgabe von zum Beispiel  und  wird:

Im Beispiel der Abbildung 6 ist . Sechsecke dieser Art kšnnen immer fŸr ein Parkett mit Translationssymmetrie verwendet werden (Abb. 7). Wir werden diese Parkette daher im Folgenden nicht mehr erwŠhnen.

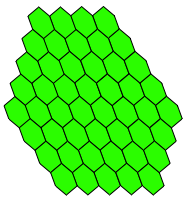
Abb. 7: Translationssymmetrie

Mit der Bedingung  erhalten wir fŸr unser Sechseck einen achsensymmetrischen Sonderfall (Abb. 8).

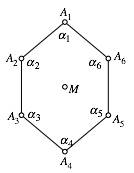
Abb. 8: Achsensymmetrischer Sonderfall

Wir haben dann nur noch  als freien Parameter und es ist:

4     SonderfŠlle

Wir werden nun SonderfŠlle ansehen, in welchen  und/oder  Teiler des vollen Winkels  sind. Die Auflistung ist weder systematisch noch vollzŠhlig (es gibt ja unendlich viele Teiler des vollen Winkels).

4.1    HŠlfte des vollen Winkels

Es ist also . Das Sechseck wird zu einem Parallelogramm mit dem SeitenverhŠltnis 2 : 1.

4.1.1   Symmetrischer Fall

Wenn dieses Parallelogramm zusŠtzlich ein Rechteck ist (achsensymmetrischer Fall), gibt es viele Mšglichkeiten, die auch in der Praxis verwendet werden. Im Folgenden einige Beispiele.

Abb. 9: Punktsymmetrie

Abb. 10: Klassisch

Abb. 11: Fischgrat

 

Die Abbildung 12 zeigt ein Parkett mit vierteiliger Rotationssymmetrie.

Abb. 12: Vierteilige Rotationssymmetrie

4.1.2   Allgemeiner Fall

Die Abbildungen 13 bis 15 zeigen die den Abbildungen 9 bis 11 entsprechenden Beispiele fŸr ein beliebiges Parallelogramm. Nun mŸssen wir auch mit spiegelbildlichen Parallelogrammen arbeiten.

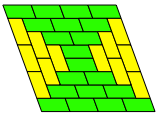
Abb. 13: Punktsymmetrie

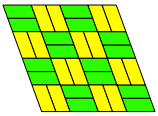
Abb. 14: Klassisch

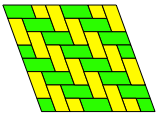
Abb. 15: Fischgrat

4.1.3   SonderfŠlle

4.1.3.1  FŸnfteilig

Wir wŠhlen nun zusŠtzlich . Damit kšnnen wir eine fŸnfteilige Rotationssymmetrie erreichen (Abb. 16).

Abb. 16: FŸnfteilige Rotationssymmetrie

 

4.1.3.2  Tetraeder-Netz

Wir wŠhlen nun . Das Parallelogramm kann in vier gleichseitige Dreiecke zerlegt werden und ist dann ein Netz (Abwicklung, Schnittmuster) des regulŠren Tetraeders (Abb. 17).

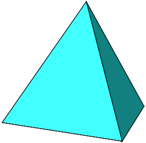
Abb. 17: Tetraeder

Die Abbildung 18 zeigt die drei mšglichen Tetraeder-Netze.

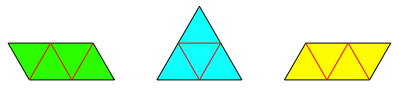
Abb. 18: Tetraeder-Netze

Das Parallelogramm erlaubt verschiedene Parkette. Im Folgenden einige Beispiele. Die Beispiele kšnnen als unendliche †berlagerung des Tetraeders gesehen werden.

Abb. 19: Dreiteilige Rotationssymmetrie

Abb. 20: Sechsteilige Rotationssymmetrie

Abb. 21: Dreiteilige Rotationssymmetrie

Abb. 22: WŸrfelmuster

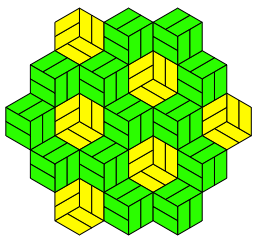
Abb. 23: Tante Annas KŸchenboden

4.2    Drittel des vollen Winkels

Nun ist . Wir kšnnen auf jeden Fall ein Parkett mit dreiteiliger Rotationssymmetrie auslegen.

4.2.1   Symmetrischer Fall

Im symmetrischen Fall ist auch , das Sechseck ist regelmŠ§ig und wir erhalten das klassische hexagonale Parkett der Abbildung 1.

4.2.2   Allgemeiner Fall

Im allgemeinen Fall kšnnen wir ein Parkett mit dreiteiliger Rotationssymmetrie gemŠ§ den Abbildungen 3 und 5 auslegen.

4.2.3   SonderfŠlle

4.2.3.1  Rechter Winkel

Nun sei  ein rechter Winkel.

Die Abbildung 24 zeigt das Parkett mit dreiteiliger Rotationssymmetrie.

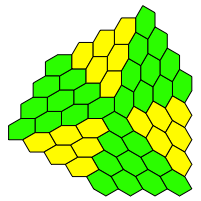
Abb. 24: Dreiteilige Rotationssymmetrie

Im Parkett der Abbildung 25 haben wir eine vierteilige Rotationssymmetrie.

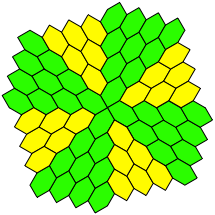
Abb. 25: Vierteilige Rotationssymmetrie

4.2.3.2  FŸnftel des vollen Winkels

Mit  kšnnen wir eine fŸnfteilige Drehsymmetrie erarbeiten (Abb. 26).

Abb. 26: FŸnfteilige Rotationssymmetrie

4.2.3.3  Sechstel des vollen Winkels

Der Fall  entspricht inhaltlich dem Parallelogramm des Tetraeder-Netzes (Abschnitt 4.1.3.2).

4.2.3.4  Siebtel des vollen Winkels

Der Winkel  lŠsst sich nicht mit Zirkel und Lineal konstruieren. Und er fŸhrt auf ein nicht konvexes Sechseck. Die Abbildung 27 zeigt das zugehšrige Parkett mit dreiteiliger Rotationssymmetrie, die Abbildung 28 den Fall mit siebenteiliger Rotationssymmetrie.

Abb. 27: Dreiteilige Rotationssymmetrie

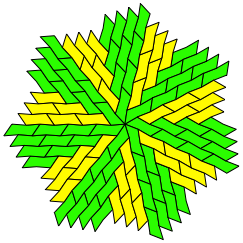
Abb. 28: Siebenteilige Rotationssymmetrie

4.2.3.5  Achtel des vollen Winkels

Mit  ergeben sich ebenfalls nicht konvexe Parkettsteine.

Abb. 29: Achtteilige Rotationssymmetrie

Interessanterweise unterliegen wie bei diesen nicht konvexen Beispielen einer optischen TŠuschung: die Sechsecke sind scheinbar nicht mehr gleichseitig. In der Abbildung 30a erscheint etwa die Seite a6 deutlich lŠnger als die Seite a5. Abgreifen mit dem Zirkel bestŠtigt aber die gleiche LŠnge aller sechs Seiten.

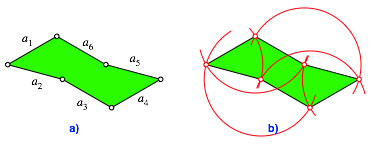
Abb. 30: Gleichseitiges Sechseck?

4.3    Viertel des vollen Winkels

Nun sei  ein rechter Winkel.

4.3.1   Symmetrischer Fall

Die Abbildung 31 zeigt den Parkettstein des symmetrischen Falls. Das Sechseck kann so unterteilt werden, dass es ein Netz eines unregelmŠ§igen Tetraeders wird. Dieses Tetraeder ist ein so genanntes Orthoschem (siehe Orthoschem.htm oder Orthoschem.pdf). Es ist die konvexe HŸlle dreier aufeinanderfolgender paarweise orthogonaler Strecken gleicher LŠnge.

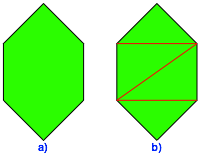
Abb. 31: Netz des Orthoschems

Das Orthoschem kann in einen WŸrfel eingepasst werden (Abb. 32).

Abb. 32: Orthoschem im WŸrfel

 

Die Abbildung 33 zeigt das zugehšrige Parkett mit vierteiliger Rotationssymmetrie.

Abb. 33: Symmetrien des Quadrates

4.3.2   Asymmetrisches Beispiel

Wir wŠhlen . Das gestattet ein Parkett mit vierteiliger Rotationssymmetrie (Abb. 34) oder ein Parkett mit 13-teiliger Rotationssymmetrie (Abb. 35).

Abb. 34: Vierteilige Rotationssymmetrie

Abb. 35: 13-teilige Rotationssymmetrie

Der Vergleich der Abbildungen 34 und 35 zeigt, dass die Figuren beide aus den gleichen Sektoren der Abbildung 36 zusammengesetzt sind.

Abb. 36: Sektor

In der Abbildung 34 haben wir vier Sektoren, die am ãdickenÒ Ende (links in der Abbildung 36) verbunden sind, in der Abbildung 35 aber 13 Sektoren, die am schmalen Ende (rechts in der Abbildung 36) verheftet sind. Die roten Punkte liegen in den jeweiligen Zentren der Figuren.

 

Websites

Orthoschem:

http://www.walser-h-m.ch/hans/Miniaturen/O/Orthoschem/Orthoschem.htm

http://www.walser-h-m.ch/hans/Miniaturen/O/Orthoschem/Orthoschem.pdf