Hans Walser, [20210124]
Satz von Haga
Idee und Anregung: Alfred Hoehn, Basel
1 Worum geht es?
Herstellung pythagoreischer Dreiecke mittels Origamifalten
2 Erinnerung
Pythagoreische Dreiecke kšnnen wie folgt konstruiert werden: Es seien m und n teilerfremde natźrliche Zahlen ungleicher ParitŠt mit m > n. Dann sind
![]() (1)
(1)
die Seiten eines primitiven pythagoreischen Dreiecks.
Die Formeln (1) werden als babylonische Formeln bezeichnet.
Beispiele:
|
m |
n |
a |
b |
c |
|
2 |
1 |
3 |
4 |
5 |
|
3 |
2 |
5 |
12 |
13 |
|
4 |
1 |
15 |
8 |
17 |
|
4 |
3 |
7 |
24 |
25 |
|
5 |
2 |
21 |
20 |
29 |
|
5 |
4 |
9 |
40 |
41 |
Tab. 1: Beispiele
Bemerkung ohne Beweis: Mit den babylonischen Formeln kšnnen sŠmtliche pythagoreischen Dreiecke generiert werden.
3 Faltprozess
Die pythagoreischen Dreiecke lassen sich durch Origami-Falten herstellen. Wir illustrieren das Vorgehen exemplarisch fźr den Fall m = 3 und n = 2.
Aus einem Quadratraster schneiden wir ein m×m-Quadrat (Abb. 1a). Am oberen Rand zŠhlen wir von rechts her n Einheiten ab und falten die rechte untere Ecke auf diesen Punkt (Abb. 1b). Von der Oberseite der QuadratflŠche bleiben zwei rechtwinklige Dreiecke sichtbar. Sie sind Šhnlich (gleiche Winkel).
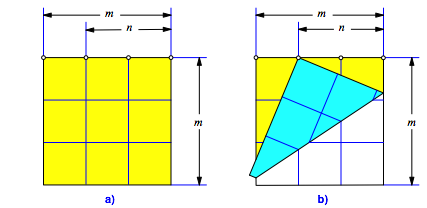
Abb. 1: Ecke Auffalten
Beides sind pythagoreische Dreiecke (Satz von Hages).
Das am linken Rand unten vorstehende kleine Schnipsel ist Šhnlich zu den beiden Dreiecken und damit ebenfalls ein pythagoreisches Dreieck.
4 Beweis
Wir fźhren den Beweis fźr das rechtwinklige Dreieck rechts oben. Seine Seiten bezeichnen wir mit x, y, z (Abb. 2).
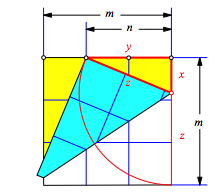
Abb. 2: Beweisfigur
Es ist:
 (2)
(2)
Das Gleichungssystem (3) hat fźr x, y, z die Lšsungen (auf einen gemeinsamen Nenner gebracht):
![]() (3)
(3)
Somit ist:
![]() (4)
(4)
Wegen (1) hat das Dreieck die Form eines pythagoreischen Dreiecks. Dies war zu zeigen.
Literatur
Hoehn, Alfred und Huber, Martin (2005): Pythagoras. Erinnern Sie sich? Zźrich, Orell Fźssli-Verlag 2005. ISBN 3-280-04040-X
Hoehn, Alfred und Walser, Hans (2003): Gittergeometrie und pythagoreische Dreiecke. Praxis der Mathematik (5/45), 215-217.
Website
Hans Walser: Pythagoreische Dreiecke falten
https://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dr_falten/Pyth_Dr_falten.htm