Hans Walser, [20100803a]

Halbieren mit dem goldenen Schnitt

1 Worum geht es?

Es wird eine Spielerei vorgeführt, in welcher eine Strecke in einem bestimmten Verhältnis geteilt werden kann. Beim Halbieren tritt der goldene Schnitt auf.

2 Einstiegsbeispiel

Wie kann eine Strecke AB gedrittelt werden, wenn folgende Hilfsmittel zur Verfügung stehen?

- Halbieren einer Strecke

- Gerade durch zwei Punkte

- Schneiden zweier Geraden

Das geht so:

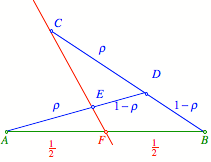
Wir wählen einen Hilfspunkt C außerhalb der Geraden AB. Dann sei D der Mittelpunkt der Strecke BC und E der Mittelpunkt der Strecke AD. Die Gerade CE schneidet AB im Drittelspunkt F.

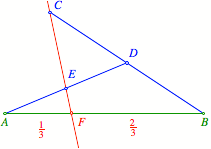
Zwei Mal halbieren

Der Beweis ergibt sich durch Einzeichnen einer Parallelen zu CE durch D und Anwendung von Strahlensätzen.

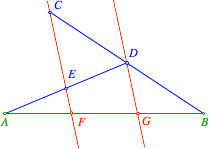
Beweisfigur

3 Verallgemeinerung

Wir nehmen nun an, wir könnten in zwei vorgegebenen Verhältnissen und teilen.

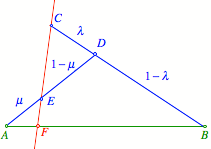
Zwei Teilverhältnisse möglich

In welchem Verhältnis teilt F die Strecke AB?

Wir zeichnen eine Parallele zu CE durch D ein und bezeichnen gemäß Figur.

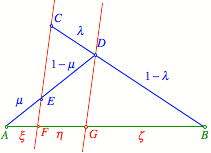
Bezeichnungen

Es ist . Gesucht ist . Auf Grund der Strahlensätze ist:

Wegen ergibt sich:

4 Sonderfall in der Verallgemeinerung

Wir nehmen nun an, dass wir nur in einem Teilverhältnis teilen können, also . Damit wird:

Im Intervall wächst monoton von 0 bis 1.

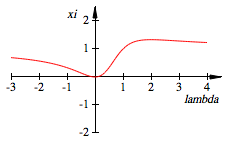
Das resultierende Teilverhältnis

Es ist zum Beispiel (vgl. Einstiegsbeispiel) .

5 Vorgegebene Ziel-Teilverhältnisse

Wir wollen nun vorgeben und suchen passende . Wir erhalten:

Insbesondere:

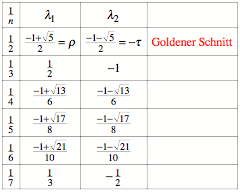
Lösungen

Ich gebe zu, dass es nicht sehr elegant ist, mit dem goldenen Schnitt eine Strecke zu halbieren.

Halbieren mit dem goldenen Schnitt

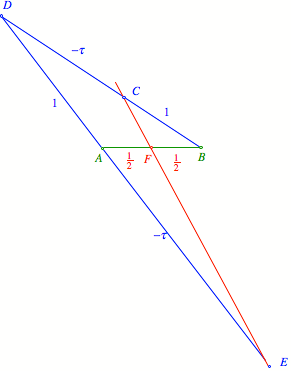
Halbieren mit der negativen Lösung beim goldenen Schnitt