Hans Walser, [20221220]

Halbstreifen

Idee und Anregung: Peter Gallin, Zürich

1 Worum geht es?

Kombinatorische Spielerei in Halbstreifen

Link zur Fibonacci-Folge

2 Halbstreifen der Breite 2

2.1 Streifen und Rechtecke

Wir arbeiten in einem nach rechts offenen Halbstreifen der Breite 2 (Abb. 1).

Abb. 1: Halbstreifen

Diesen Halbstreifen wollen wir von links her bis zur Länge n mit 1×2-Rechtecken (Abb. 2) belegen. Die Rechtecke quer zur Laufrichtung des Streifens zeichnen wir rot, die Rechtecke längs der Laufrichtung gelb.

Abb. 2: Rechtecke

2.2 Problemstellung

Wie viele Lösungen gibt es?

2.3 Beispiele

Für n = 0 erhalten wir nur eine Lösung, nämlich den leeren Streifen (Abb. 3.0).

Abb. 3.0: Leerer Streifen

Für n = 1 gibt es ebenfalls nur eine Lösung (Abb. 3.1). Das Rechteck steht quer zur Laufrichtung.

Abb. 3.1: Querstehendes Rechteck

Für n = 2 gibt es nun zwei Lösungen (Abb. 3.2). Aus Platzgründen (siehe später) sind die Halbstreifen der beiden Lösungen satt aneinandergesetzt.

Zu diesen beiden Lösungen kommen wir wie folgt: Wir können einerseits beim leeren Halbstreifen (Abb. 3.0) zwei gelbe Rechtecke in Laufrichtung einfügen oder aber im Halbstreifen mit bereits einem Rechteck (Abb. 3.1) ein zusätzliches rotes querstehendes Rechteck einfügen.

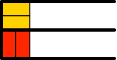
Abb. 3.2: Zwei Lösungen

Für n = 3 gibt es drei Lösungen (Abb. 3.3). Zu diesen drei Lösungen kommen wir wie folgt: Wir können einerseits beim Halbstreifen mit nur einem Rechteck (Abb. 3.1) zwei gelbe Rechtecke in Laufrichtung einfügen oder aber in den beiden Halbstreifen mit zwei Rechtecken (Abb. 3.2) je ein zusätzliches rotes querstehendes Rechteck einfügen.

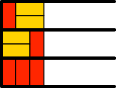
Abb. 3.3: Drei Lösungen

Für n = 4 wird es spannend. Es gibt nicht, wie vielleicht erwartet, 4 Lösungen, sondern deren 5 (Abb. 3.4). Wir können nämlich einerseits bei den beiden Halbstreifen mit zwei Rechtecken (Abb. 3.2) je zwei zusätzliche gelbe Rechtecke in Laufrichtung einfügen oder aber in den drei Halbstreifen mit drei Rechtecken (Abb. 3.3) je ein zusätzliches rotes querstehendes Rechteck einfügen.

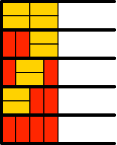
Abb. 3.4: Fünf Lösungen

Für n = 5 gibt es entsprechend 3 + 5 = 8 Lösungen (Abb. 3.5). Wir können einerseits bei den drei Halbstreifen mit drei Rechtecken (Abb. 3.3) je zwei zusätzliche gelbe Rechtecke in Laufrichtung einfügen oder aber in den fünf Halbstreifen mit vier Rechtecken (Abb. 3.4) je ein zusätzliches rotes querstehendes Rechteck einfügen.

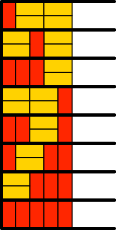
Abb. 3.5: Acht Lösungen

Für n = 6 gibt es 5 + 8 = 13 Lösungen (Abb. 3.6).

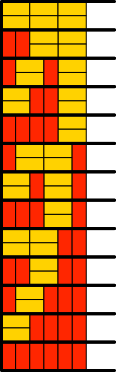
Abb. 3.6: 13 Lösungen

Für n = 7 erhalten wir 8 + 13 = 21 Lösungen (Abb. 3.7).

Abb. 3.7: 21 Lösungen

2.4 Übersicht

Die Tabelle 1 gibt eine Zusammenstellung. Es handelt sich offensichtlich um Fibonacci-Zahlen.

n	0	1	2	3	4	5	6	7
Anzahl Lösungen	1	1	2	3	5	8	13	21

Tab. 1: Fibonacci-Zahlen

2.5 Rekursion

Die Anzahl a_n der Lösungen für die Länge n zu berechnen wir so (Abb. 4):

Wir greifen wir zurück auf die Lösungen der Länge n – 2. Diesen Lösungen (es sind a_n–2 Stück) setzen wir zwei Rechtecke in der Laufrichtung an.

Dann greifen wir zurück auf die Lösungen der Länge n – 1. Diesen Lösungen (es sind a_n–1 Stück) setzen wir ein Rechtecke quer zur Laufrichtung an.

Damit erhalten wir insgesamt a_n–1 + a_n–2 Lösungen der Länge n.

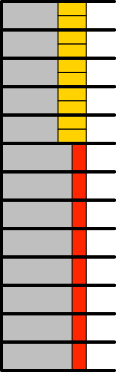
Abb. 4: Rekursion

Es gilt also die Rekursion:

a_n = a_n–1 + a_n–2

Dies ist die Fibonacci-Rekursion. Die beiden Startwerte sind in unserem Beispiel: a₀ = 1 und a₁ = 1.

2.6 Von links nach rechts

Die Laufrichtung von links nach rechts ist wesentlich. Andernfalls hätten wir Mehrfachlösungen.

So sind zum Beispiel in der Abbildung 3.3 für n = 3 das erste und das zweite Beispiel gleich, aber in umgekehrter Laufrichtung (Abb. 5.3). Ohne Berücksichtigung der Laufrichtung bleiben also nur zwei Lösungen.

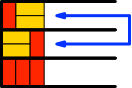
Abb. 5.3: Umgekehrte Laufrichtung. Noch zwei Lösungen

Für n = 4 (Abb. 3.4) bleiben ohne Berücksichtigung der Laufrichtung noch 4 Lösungen (Abb. 5.4).

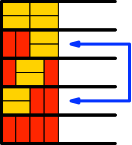
Abb. 5.4: Umgekehrte Laufrichtung. Noch vier Lösungen

Für n = 5 (Abb. 3.5) bleiben ohne Berücksichtigung der Laufrichtung noch 5 Lösungen (Abb. 5.5).

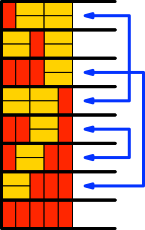
Abb. 5.5: Noch fünf Lösungen

Für n = 6 (Abb. 3.6) bleiben noch 9 Lösungen (Abb. 5.6).

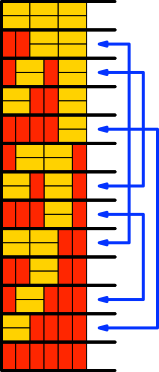
Abb. 5.6: Noch neun Lösungen

Für n = 7 (Abb. 3.7) bleiben noch zwölf Lösungen (Abb. 5.7).

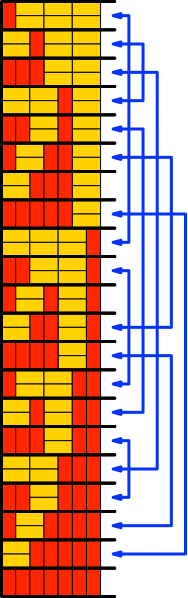
Abb. 5.7: Noch zwölf Lösungen

Der Autor weiß nicht, welche Gesetzmäßigkeit dahintersteckt.

3 Halbstreifen der Breite 3

3.1 Ausgangslage

Wir arbeiten nun in einem nach rechts offenen Halbstreifen der Breite 3 (Abb. 6).

Abb. 6: Halbstreifen

Diesen Halbstreifen wollen wir von links her bis zur Länge n mit 1×3-Rechtecken (Abb. 7) belegen. Die Rechtecke quer zur Laufrichtung des Streifens zeichnen wir rot, die Rechtecke längs der Laufrichtung gelb.

Abb. 7: Rechtecke

3.2 Problemstellung

Wie viele Lösungen gibt es?

3.3 Beispiele

Für n = 0 erhalten wir nur eine Lösung, nämlich den leeren Streifen (Abb. 8.0).

Abb. 8.0: Leerer Streifen

Für n = 1 und n = 2 gibt es ebenfalls nur je eine Lösung (Abb. 8.1 und 8.2). Die Rechtecke stehen quer zur Laufrichtung.

Abb. 8.1: Querstehendes Rechteck

Abb. 8.2: Zwei querstehende Rechtecke

Für n = 3 gibt es nun zwei Lösungen (Abb. 8.3). Aus Platzgründen sind die Halbstreifen der beiden Lösungen satt aneinandergesetzt. Zu diesen beiden Lösungen kommen wir wie folgt: Wir können einerseits beim leeren Halbstreifen (Abb. 8.0) drei gelbe Rechtecke in Laufrichtung einfügen oder aber im Halbstreifen mit bereits zwei Rechtecken (Abb. 8.2) ein zusätzliches rotes querstehendes Rechteck einfügen.

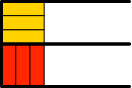
Abb. 8.3: Zwei Lösungen

Für n = 4 gibt es drei Lösungen (Abb. 8.4). Zu diesen drei Lösungen kommen wir wie folgt: Wir können einerseits beim Halbstreifen mit nur einem Rechteck (Abb. 8.1) drei gelbe Rechtecke in Laufrichtung einfügen oder aber in den beiden Halbstreifen mit drei Rechtecken (Abb. 8.3) je ein zusätzliches rotes querstehendes Rechteck einfügen.

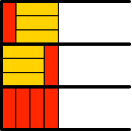
Abb. 8.4: Drei Lösungen

Für n = 5 gibt es vier Lösungen (Abb. 8.5). Wir können einerseits beim Halbstreifen mit zwei Rechtecken (Abb. 8.2) drei gelbe Rechtecke in Laufrichtung einfügen oder aber in den drei Halbstreifen mit je vier Rechtecken (Abb. 8.4) je ein zusätzliches rotes querstehendes Rechteck einfügen.

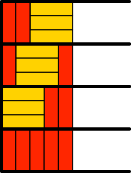
Abb. 8.5: Vier Lösungen

Für n = 6 gibt es sechs Lösungen (Abb. 8.6). Wir können einerseits bei den beiden Halbstreifen mit drei Rechtecken (Abb. 8.3) drei gelbe Rechtecke in Laufrichtung einfügen oder aber in den vier Halbstreifen mit je fünf Rechtecken (Abb. 8.5) ein zusätzliches rotes querstehendes Rechteck einfügen.

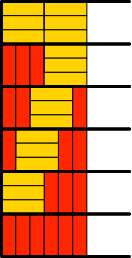
Abb. 8.6: Sechs Lösungen

Für n = 7 gibt es entsprechend 3 + 6 = 9 Lösungen (Abb. 8.7).

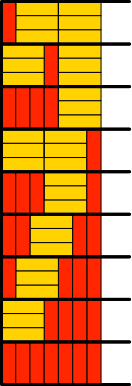
Abb. 8.7: Neun Lösungen

Für n = 8 gibt es 4 + 9 = 13 Lösungen (Abb. 8.8)

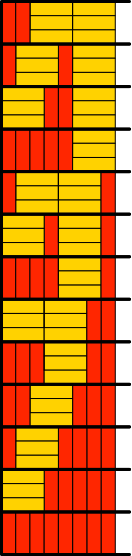
Abb. 8.8: 13 Lösungen

3.4 Rekursion

Die Anzahl a_n der Lösungen für die Länge n zu berechnen wir so (Abb. 9):

Wir greifen wir zurück auf die Lösungen der Länge n – 3. Diesen Lösungen (es sind a_n–3 Stück) setzen wir drei Rechtecke in der Laufrichtung an.

Dann greifen wir zurück auf die Lösungen der Länge n – 1. Diesen Lösungen (es sind a_n–1 Stück) setzen wir ein Rechtecke quer zur Laufrichtung an.

Damit erhalten wir insgesamt a_n–1 + a_n–3 Lösungen der Länge n.

Abb. 9: Rekursion

Es gilt also die Rekursion:

a_n = a_n–1 + a_n–3

Dies ist eine verallgemeinerte Fibonacci-Rekursion. Die beiden Startwerte sind in unserem Beispiel: a₀ = 1, a₁ = 1 und a₂ = 1.

Die Tabelle 2 gibt die ersten Daten.

n	an	n	an
0	1	10	28
1	1	11	41
2	1	12	60
3	2	13	88
4	3	14	129
5	4	15	189
6	6	16	277
7	9	17	406
8	13	18	595
9	19	19	872

Tab. 2: Erste Daten

3.5 Ein Grenzwert

In der Tabelle 3 sind zusätzlich die Quotienten a_n+1/ a_n eingetragen. Wir vermuten einen Grenzwert.

n	an	an+1/ an	n	an	an+1/ an
0	1	1	10	28	1.464285714
1	1	1	11	41	1.463414634
2	1	2	12	60	1.466666667
3	2	1.5	13	88	1.465909091
4	3	1.333333333	14	129	1.465116279
5	4	1.5	15	189	1.465608466
6	6	1.5	16	277	1.465703971
7	9	1.444444444	17	406	1.465517241
8	13	1.461538462	18	595	1.465546218
9	19	1.473684211	19	872	1.465596330

Tab. 3: Quotienten

Der Grenzwert ist die reelle Lösung der kubischen Gleichung:

x³ = x² + 1

Es ist: