Hans Walser, [20170911]

Hamiltonkreis im Gitterwürfel

Anregung: Heinz Schumann, Weingarten

1 Fragestellung

Die Abbildung 1a zeigt einen 2×2×2-Gitterwürfel (wir zählen die Gitterpunkte, nicht die Seitenlängen („Zaunpfahl-Problem“)) mit einem roten Hamiltonkreis. Dies ist ein geschlossener Weg auf den schwarzen Kanten, der jeden Gitterpunkt genau einmal trifft.

Gibt es einen Hamiltonkreis auf dem 3×3×3-Gitterwürfel der Abbildung 1b? Die Leserin ist eingeladen, bei der Abbildung 1b einige Versuche zu machen.

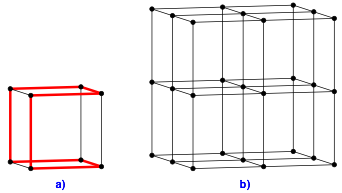
Abb. 1: Fragestellung

Die Abbildung 2 zeigt einen Hamiltonkeis auf einem 4×4×4-Gitterwürfel. Die Leserin ist eingeladen, haptisch nachzuprüfen.

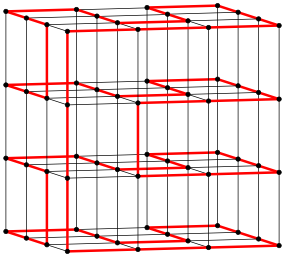
Abb. 2: Hamiltonkreis

2 Eine Paritätsfrage

Bei Versuchen, in den Gitterwürfel der Abbildung 1b einen Hamiltonkreis einzuzeichnen, stellen wir fest, dass es immer bis auf einen Gitterpunkt geht. Das lässt vermuten, dass wir es mit einem Paritätsproblem zu tun haben.

Tatsächlich werden wir sehen:

Mit einer geraden Zahl g gibt es im g×g×g-Gitterwürfel immer einen Hamiltonkreis.
Mit einer ungeraden Zahl u gibt es im u×u×u-Gitterwürfel keinen Hamiltonkreis.

3 Dimensionsfrage

Die Abbildung 3 zeigt das Analogon zur Abbildung 1 in der Ebene.

Abb. 3: Analogon in der Ebene

Im 2×2-Gitterquadrat haben wir einen Hamiltonkreis (Abb. 3a), im 3×3-Gitterquadrat (Abb. 3b) gibt es keinen. Es bleibt immer ein Gitterpunkt übrig.

Die Abbildung 4 zeigt ein 4×4-Gitterquadrat mit Hamiltonkreis.

Abb. 4: Gitterquadrat mit Hamiltonkreis

Wir können unsere Vermutungen verallgemeinern:

In der Dimension 1 gibt es keine Hamiltonkreise.

In den Dimensionen n >1 gilt:

Mit einer geraden Zahl g gibt es im gⁿ-Gitter-n-Hyperwürfel immer einen Hamiltonkreis.
Mit einer ungeraden Zahl u gibt es im uⁿ-Gitter-n-Hyperwürfel keinen Hamiltonkreis.

4 Ausschluss der ungeraden

Mit einer ungeraden Zahl u ist auch uⁿ eine ungerade Zahl. Der uⁿ-Gitter-n-Hyperwürfel hat also eine ungerade Anzahl von Gitterpunkten. Wir färben nun die Gitterpunkte abwechslungsweise rot und blau (Abb. 5).

Das geht in beliebigen Dimensionen, da die Gitterpunkte und Kanten eines Gitter-n-Hyperwürfel einen paaren oder bipartiten Graphen bilden. Um dies einzusehen, verwenden wir kartesische Koordinaten für die Gitterpunkte. Die Koordinatenachsen seien parallel zu den Gitterlinien und die Einheit die Maschenbreite des Gitters. Der Ursprung sei eine Ecke des Gitterwürfels. Die Koordinaten der Gitterpunkte im Gitterwürfel sind also nichtnegative ganze Zahlen in .

Die Summen sind entweder gerade oder ungerade. Das gibt eine Klasseneinteilung der Punkte. Wir färben die Punkte entsprechend rot oder blau. Zwei durch eine Kante verbundene Punkte haben verschiedene Farben, weil sie sich in genau einer Koordinate um 1 unterscheiden.

Da die Gesamtzahl der Gitterpunkte ungerade ist, kann die Anzahl der blauen Gitterpunkte nicht gleich der Anzahl der roten Gitterpunkte sein.

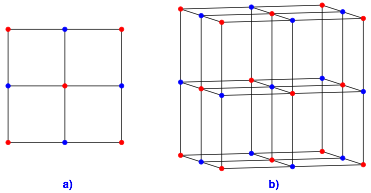
Abb. 5: Rot-blau-Färbung

Ein Hamiltonkreis durchläuft abwechslungsweise rote und blaue Punkt. Er ist also eine geschlossene Perlenkette mit abwechslungsweise roten und blauen Perlen. Daher hat es gleich viele rote wie blaue Perlen. Widerspruch.

5 Einschluss der geraden

Für eine beliebige (particular but not special) gerade Zahl g geben wir konstruktiv eine Lösung mit Induktion über die Dimension n.

Für n = 2 haben wir die „Heizschlangen“-Lösung (Abb. 6 für g = 10).

Abb. 6: Heizschlangen

Für den Schritt in die Dimension n = 3 arbeiten wir mit g ebenen Heizschlangen, die an einer Ecke etwas geöffnet sind. Und zwar nehmen wir 2 geöffnete ebene Heizschlangen vom Typ der Abbildung 7a und geöffnete ebene Heizschlangen vom Typ der Abbildung 7b.

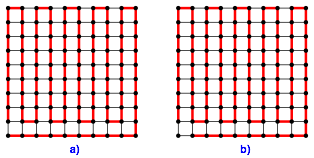
Abb.7: Geöffnete Heizschlangen

Nun stapeln wir diese g ebenen Heizschlangen senkrecht, also im Sinne der neuen, dritten, Dimension, aufeinander. Zuunterst und zuoberst je ein Exemplar der Abbildung 7a, dazwischen die anderen. Die unterste und die oberste Lage verbinden wir mit einer durchgehenden senkrechten Steigleitung an den äußersten Ecken. Diese trifft auch alle freistehenden Gitterpunkte der Heizschlangen der Abbildung 7b. Und nun verbinden wir abwechslungsweise hinter und neben dieser durchgehenden Steigleitung je zwei der ebenen Heizschlangen mit einer Steigleitung der Höhe 1. Das Verfahren ist bereits in der Abbildung 2 (für g = 4) illustriert.

Für den Schritt von der Dimension auf die Dimension n arbeiten wir mit g Lösungen für die Dimension . Wir wählen je eine Ecke und entfernen dort bei zwei Lösungen eine der beiden zum Hamiltonkreis gehörenden roten Kanten und bei den restlichen Lösungen beide zum Hamiltonkreis gehörenden roten Kanten, analog zur Abbildung 7. Dann schichten wir die Lösungen senkrecht im Sinne der n-ten Dimension so aufeinander, dass die bearbeiteten Ecken übereinander liegen, die schwarzen Kanten mit den nun fehlenden zum Hamiltonkreis gehörenden roten Kanten parallel sind und zudem zuunterst und zuoberst die beiden Sonderfälle liegen. Dann verbinden wir unten und oben mit einer durchgehenden Steigleitung und die anderen Schichten mit Steigleitungen der Höhe 1. So erhalten wir eine Lösung für die Dimension n.

6 Varianten

Es gibt auch andere Lösungen. Die Abbildungen 8a bis 8c zeigen Varianten zur Lösung der Abbildung 2. Eine ist allerdings falsch. Welche?

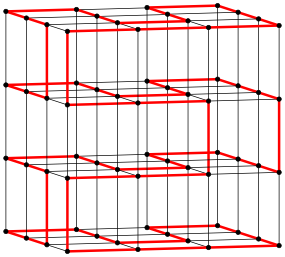
Abb. 8a: Variante

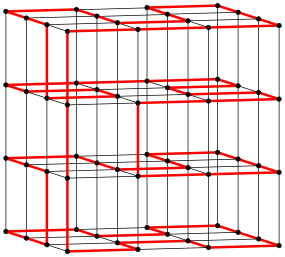
Abb. 8b: Variante

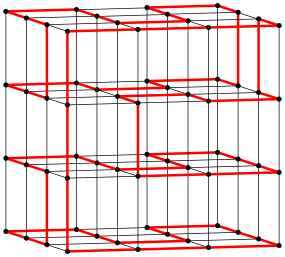
Abb. 8c: Variante

Die Abbildung 9a zeigt eine Lösung für g = 2 und die Dimension n = 4 nach dem oben beschriebenen Induktionsschritt.

Abb. 9a: Vierdimensionaler Hypergitterwürfel mit Hamiltonkreis

Die Abbildung 9b zeigt eine Variante. Die Frage ist, ob es sich wirklich um eine Variante handelt oder nur um eine andere Sicht.

Abb. 9b: Variante

Die Anzahl der Lösungen zu gegebenem g und gegebener Dimension n ist mir nicht bekannt. Ein schönes kombinatorisches Problem.