Hans Walser, [20170912]

Hamiltonkreis im Gitterrechteck

Anregung: Heinz Schumann, Weingarten

1 Gitterrechteck

In einem Karoraster zeichnen wir ein Gitterrechteck oder speziell ein Gitterquadrat (Abb. 1).

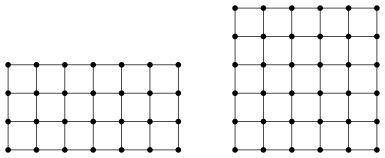
Abb. 1: Gitterrechteck und Gitterquadrat

2 Hamiltonkreis

Nun suchen wir einen geschlossenen Weg, der jeden Gitterpunkt genau einmal trifft. Die Abbildung 2 zeigt Beispiele.

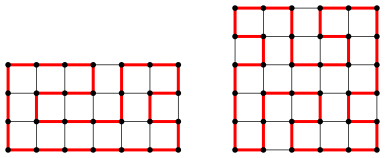
Abb. 2: Hamiltonkreise

Solche Wege werden als geschlossene Hamiltonwege oder kurz als Hamiltonkreise bezeichnet (Sir William Rowan Hamilton, 1805-1865, Dublin).

3 Wie viele Hamiltonkreise gibt es?

Zeichne verschiedene Hamiltonkreise in die Gitterrechtecke der Abbildung 3?

Wie viele Hamiltonkreise gibt es?

Abb. 3: Hamiltonkreise?

Zeichne verschiedene Hamiltonkreise in die Gitterquadrate der Abbildungen 4 und 5.

Wie viele Hamiltonkreise gibt es?

Abb. 4: Hamiltonkreise in Gitterquadraten?

Abb. 5: Hamiltonkreise in Gitterquadraten?

4 Flächen im Hamiltonkreis

Da die Hamiltonkreise geschlossen sind, können wir sie ausmalen. Die Abbildung 6 zeigt zwei verschiedene ausgemalte Hamiltonkreise im Gitterrechteck der Abbildung 1. Welche Fläche ist die größere? Wie steht es bei anderen Hamiltonkreisen in diesem Gitterrechteck?

Abb. 6: Fläche im Hamiltonkreis?

Die Abbildung 7 zeigt zwei verschiedene ausgemalte Hamiltonkreise im Gitterquadrat der Abbildung 1. Welche Fläche ist die größere? Wie steht es bei anderen Hamiltonkreisen in diesem Gitterquadrat?

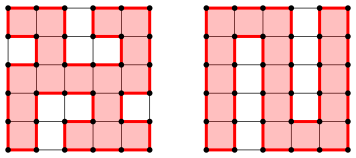
Abb. 7: Fläche im Hamiltonkreis?

5 Bearbeitung der Fragen

5.1 Gerade und ungerade

Wir färben die Gitterpunkte abwechslungsweise blau und gelb (Abb. 8).

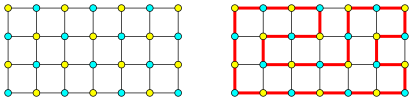
Abb. 8: Blaue und gelbe Gitterpunkte

Auf einem Hamiltonkreis hat es dann ebenfalls abwechslungsweise blaue und gelbe Gitterpunkte. Da der Hamiltonkreis geschlossen ist, haben wir gleich viele blaue wie gelbe Gitterpunkte. Die Gesamtzahl der Gitterpunkte ist daher eine gerade Zahl. Da das Gitterrechteck der Abbildung 3b und das Gitterquadrat der Abbildung 4b eine ungerade Anzahl von Gitterpunkten haben, gibt es darin keinen Hamiltonkreis.

5.2 Anzahl der Hamiltonkreise

Wir können uns auf die Gitterrechtecke und Gitterquadrate mit einer geraden Anzahl g von Gitterpunkten beschränken.

Im Beispiel der Abbildung 3a gibt es bis auf Spiegelung nur eine Lösung (Abb. 9).

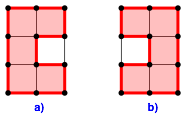
Abb. 9: Bis auf Spiegelung nur eine Lösung

Für das Beispiel der Abbildung 3c habe ich bis auf Spiegelungen und Drehungen 5 Lösungen gefunden und hoffe, dass ich keine übersehen habe (Abb. 10).

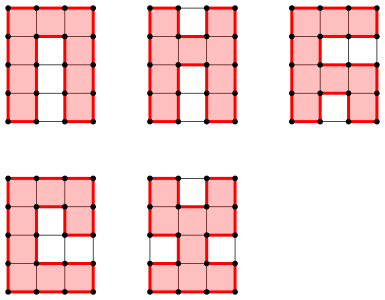
Abb. 10: Echt verschiedene Lösungen

Für das Quadratgitter der Abbildung 4a gibt es nur eine Lösung (Abb. 11).

Abb. 11: Genau eine Lösung

Für das Quadratgitter der Abbildung 4c habe ich zwei echt verschiedene Lösungen gefunden (Abb. 12).

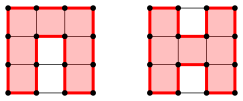
Abb. 12: Zwei echt verschiedene Lösungen

Die Abbildung 13 gibt einige Lösungen für das Quadratgitter der Abbildung 5b (siehe auch Abb. 7). Es gibt noch weitere Lösungen. Ich weiß nicht, wie viele Lösungen es insgesamt gibt.

Abb. 13: Einige Lösungen

5.3 Fläche im Hamiltonkreis

Die Fläche F kann berechnet werden, indem wir die Anzahl g der Gitterpunkte halbieren und davon 1 subtrahieren:

(1)

Um dies einzusehen, bedarf es einiger Vorbereitungen.

5.3.1 Konvexe und konkave Ecken

Wir bezeichnen mit a die Anzahl der konvexen Ecken (das sind die nach außen gerichteten Ecken des ausgemalten Hamiltonkreises) und mit c die Anzahl der konkaven Ecken (das sind die nach innen gerichteten Ecken).

Bei allen Beispielen ist a um 4 größer als c. Das ist offenbar eine Gesetzmäßigkeit.

5.3.1.1 Pinocchio

Um dies einzusehen, stellen wir uns vor, wie Pinocchio mit seiner langen Nase im positiven Sinn (Gegenuhrzeigersinn) auf dem Hamiltonkreis herumgeht (Abb. 14).

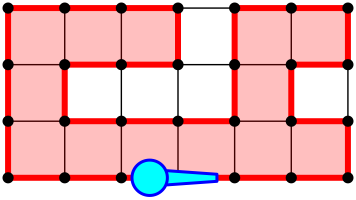
Abb. 14: Pinocchio auf dem Hamiltonkreis

Bei jeder konvexen Ecke dreht seine Nase um +90° (also im Gegenuhrzeigersinn), bei jeder konkaven Ecke dreht seine Nase um –90°. Daher dreht sich seine Nase bei einer Rundreise auf dem Hamiltonkreis insgesamt um .

Andererseits dreht sich seine Nase auf einer solchen Rundreise insgesamt um 360°.

Somit ist:

(2)

5.3.1.2 Seiten

Eine alternative Überlegung geht so: Zunächst ist jede Ecke des Gitterrechtecks oder des Gitterquadrates ein konvexe Ecke (in Abb. 15 rot markiert).

Abb. 15: Eine Seite. Gleich viele Linksabbieger wie Rechtsabbieger

Die Seiten zwischen diesen Ecken haben am Anfang und am Ende dieselbe Richtung. Bei positivem Umgang heißt das, dass die Linksabbieger (konvexe Ecken) und die Rechtsabbieger (konkave Ecken) sich die Waage halten müssen. Somit bleiben per Saldo die vier äußersten konkaven Ecken des Gitterrechtecks oder des Gitterquadrates übrig. Es gilt also erneut (2).

5.3.2 Einbetten in Quadrate

Wir umgeben jeden Gitterpunkt mit einem blauen Quadrat der Seitenlänge der Gitterquadrate. Die Abbildung 16 zeigt exemplarische Beispiele.

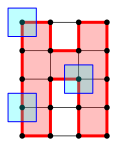
Abb. 16: Einbetten in blaue Quadrate

In einer konvexen Ecke bedeckt dieses Quadrat zu einem Viertel die rote Fläche des Hamiltonkreises, in einem Gitterpunkt mit geradlinig durchgehendem Hamiltonkreis die Hälfte und in einer konkaven Ecke drei Viertel.

Wir bezeichnen mit b die Anzahl derjenigen Gitterpunkte, in denen der Hamiltonkreis geradlinig durchläuft. Es ist dann:

(3)

Für die rote Fläche F des Hamiltonkreises gilt offensichtlich:

(4)

Wir müssen zeigen, dass (1) und (4) übereinstimmen, also:

(5)

Wir formen um und vereinfachen:

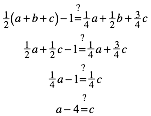(6)

Dies folgt aber aus (2). Damit ist die Formel (1) bewiesen.

Websites

Hans Walser: Hamiltonkreis im Gitterwürfel (abgerufen 12.09.2017):

www.walser-h-m.ch/hans/Miniaturen/H/Hamiltonkreis/Hamiltonkreis.htm