Hans Walser, [20100615a]
Hamming-Distanzen
Anregung: M. R., B.
1 Worum es geht
Wenn sich zwei k-stellig Zahlen an genau h Stellen unterscheiden, sagen wir, sie haben die Hamming-Distanz h.
In einem Zahlensystem mit der Basis n werden nun die Hamming-Distanzen k-stelliger Zahlen tabelliert und farblich codiert.
2 Einfźhrungsbeispiel
Wir
nehmen die vierstelligen Zahlen im Zahlensystem mit der Basis 2 (Dualzahlen).
Es ist also ![]() und
und ![]() .
.
ZunŠchst eine Liste dieser Zahlen.
|
Dezimalsystem |
Basis 4 |
|
0 |
0 |
|
1 |
1 |
|
2 |
10 |
|
3 |
11 |
|
4 |
100 |
|
5 |
101 |
|
6 |
110 |
|
7 |
111 |
|
8 |
1000 |
|
9 |
1001 |
|
10 |
1010 |
|
11 |
1011 |
|
12 |
1100 |
|
13 |
1101 |
|
14 |
1110 |
|
15 |
1111 |
Wir erhalten dazu die Distanztabelle (Hamming-Distanz) :
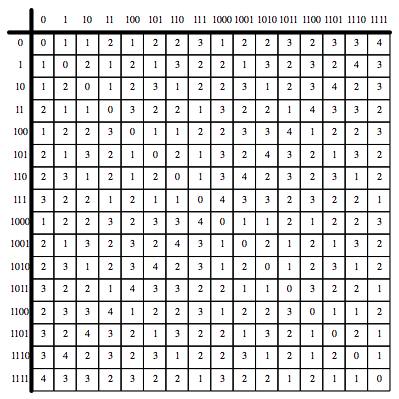
Hamming-Distanz
Wir arbeiten weiter mit der folgenden Farb-Palette.

Farb-Palette
Die Tabelle mit den Hamming-Distanzen fŠrben wir entsprechend ein. Null wird schwarz eingefŠrbt.
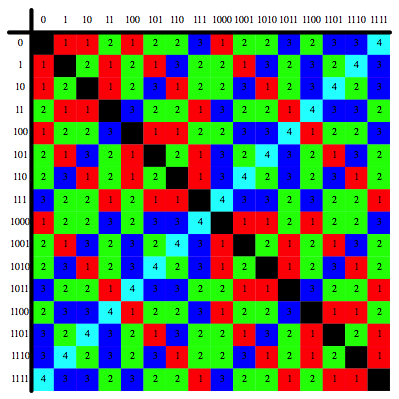
Farbliche Codierung
Schlie§lich dasselbe ohne Zahlen.

Basis 2, vierstellig
3 Beispiele
Die Beispiele sind nach der Stellenzahl geordnet
3.1 Einstellige Zahlen
Einstellige Zahlen haben zu sich selber die Hamming-Distanz 0 und zu allen anderen Zahlen die Hamming-Distanz 1.
Als Beispiel die einstelligen Zahlen zur Basis 4 und die einstelligen Dezimalzahlen.

Einstellig, Basis 4
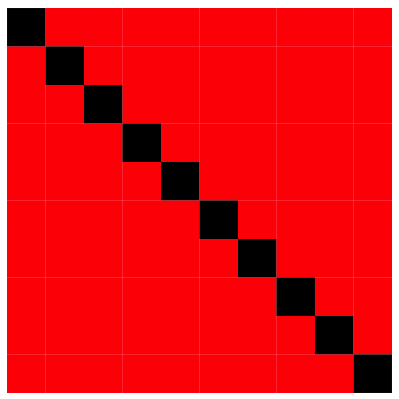
Einstellig, Dezimalzahlen
3.2 Zweistellige Zahlen
Wir haben die AbstŠnde 0, 1 und 2, also drei Farben.
3.2.1 Basis 1

Zweistellig, Basis 1
Was geht hier ab?
3.2.2 Basis 2

Zweistellige Dualzahlen
3.2.3 Basis 3

Zweistellig, Basis 3
3.2.4 Basis 4

Zweistellig, Basis 4
3.2.5 Basis 5

Zweistellig, Basis 5
3.2.6 Basis 6

Zweistellig, Basis 6
Wir erkennen eine einheitliche Muster-Struktur. Bei der Basis n haben wir lŠngs der Hauptdiagonalen (von links oben nach rechts unten) n Teilquadrate mit dem Muster der einstelligen Zahlen.
3.3 Dreistellige Zahlen
Wir haben nun vier Farben.
3.3.1 Basis 1

Dreistellig, Basis 1
3.3.2 Basis 2

Dreistellig, Basis 2
3.3.3 Basis 3

Dreistellig, Basis 3
3.3.4 Basis 4
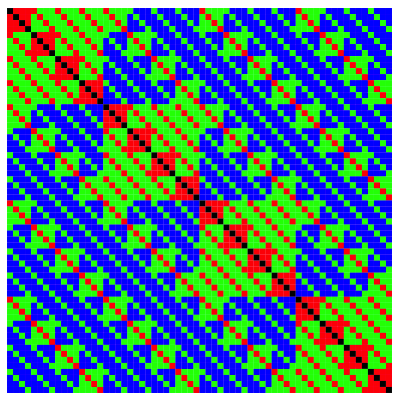
Dreistellig, Basis 4
3.4 Vierstellige Zahlen
3.4.1 Basis 1

Vierstellig, Basis 1
3.4.2 Basis 2

Vierstellig, Basis 2
3.4.3 Basis 3
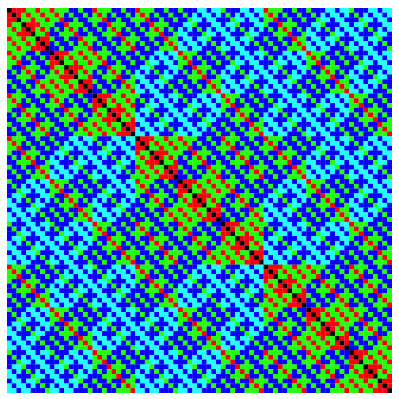
Vierstellig, Basis 3
4 Zusammenhang bei gleicher Basis
Bei
gleicher Basis gibt es einen Zusammenhang der Muster źber die Stellenzahlen hinweg.
Wir illustrieren das an der Basis ![]() und unterteilen
jeweils in
und unterteilen
jeweils in ![]() Teilquadrate.
Teilquadrate.
Fźr die
Stellenzahl ![]() ergibt sich:
ergibt sich:

Dreistellig, Basis 4, mit Unterteilung
In den ![]() Teilquadraten
haben wir źberall dieselbe Struktur, bei den Teilquadraten in der Hauptdiagonalen
sind lediglich die Farben eine Stufe niedriger. Die Teilquadrate entsprechen
der Gesamtsituation fźr
Teilquadraten
haben wir źberall dieselbe Struktur, bei den Teilquadraten in der Hauptdiagonalen
sind lediglich die Farben eine Stufe niedriger. Die Teilquadrate entsprechen
der Gesamtsituation fźr ![]() (zweistellig,
Basis 4).
(zweistellig,
Basis 4).
Diese unterteilen wir nun ebenfalls.
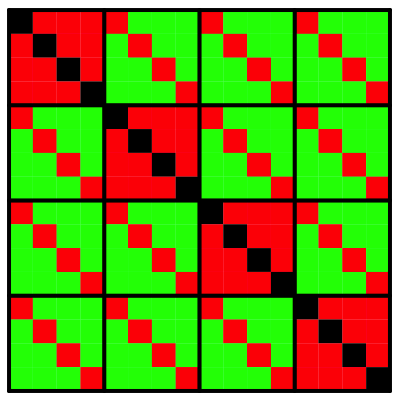
Zweistellig, Basis 4, mit Unterteilung
Die Teilquadrate
entsprechen der Gesamtsituation fźr ![]() (einstellig,
Basis 4).
(einstellig,
Basis 4).
Erneut kšnnen wir unterteilen.

Einstellig, Basis 4, mit Unterteilung