Hans Walser, [20200625]
Harmonische Folge
1 Worum geht es?
Zu zwei
gegebenen Werten 
und 
ist die
harmonische Folge gesucht.
2 Rekursion
Wir arbeiten mit dem harmonischen Mittel:
(1)
Daraus ergibt sich die Rekursion:
(2)
Zusammen mit den Startwerten kann nun die harmonische Folge rekursiv berechnet werden.
3 Explizite Formel
Wir arbeiten mit dem Ansatz (gebrochen lineare Funktion):
(3)
Einsetzen der Startwerte liefert:
(4)
Damit erhalten wir aus (3) die explizite Formel:
(5)
4 Beispiele
|
n |
an |
bn |
cn |
dn |
en |
fn |
|
1 |
1 |
1 |
1 |
1 |
5 |
4 |
|
2 |
1/2 |
6/7 |
7/6 |
5/3 |
4 |
5 |
|
3 |
1/3 |
3/4 |
7/5 |
5 |
10/3 |
20/3 |
|
4 |
1/4 |
2/3 |
7/4 |
– 5 |
20/7 |
10 |
|
5 |
1/5 |
3/5 |
7/3 |
– 5/3 |
5/2 |
20 |
|
6 |
1/6 |
6/11 |
7/2 |
– 1 |
20/9 |
* |
|
7 |
1/7 |
1/2 |
7 |
– 5/7 |
2 |
|
|
8 |
1/8 |
6/13 |
* |
– 5/9 |
20/11 |
|
|
9 |
1/9 |
3/7 |
|
– 5/11 |
5/3 |
|
|
10 |
1/10 |
2/5 |
|
– 5/13 |
20/13 |
|
* Division durch null
Tab. 1: Beispiele
5 Kreise
Die Abbildung 1 zeigt eine Folge von konzentrischen Kreisen mit Radien gemŠ§ der Folge bn der Tabelle 1.
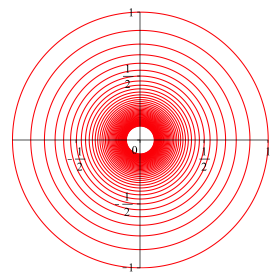
Abb. 1: Harmonische Kreisradien
Die Abbildung 2 zeigt die Kreisschar rŠumlich.
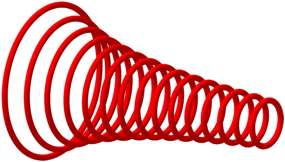
Abb. 2: RŠumliche Darstellung
6 Geometrische Folge
Die Abbildungen 3 und 4 geben im Vergleich dazu eine Kreisschar, deren Radien im Sinne einer geometrischen Folge abnehmen.
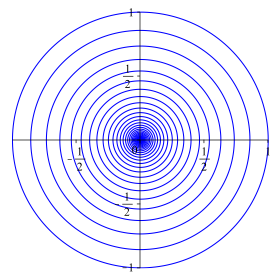
Abb. 3: Geometrisch abnehmende Kreisradien
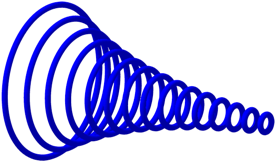
Abb. 4: RŠumliche Darstellung