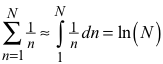Hans Walser, [20250420]

Harmonisches Mobile

1 Worum es geht

Physikalische Spielereien um die harmonische Folge und Reihe

2 Harmonische Folge und Reihe

Die harmonische Folge besteht aus den sogenannten Stammbrüchen:

Die harmonische Reihe

divergiert.

3 Aufhängung eines Mobiles

An den Enden eines Joches hängen wir zwei gleich große Massen (rot in Abb. 1) an. Das Joch und das Aufhängegelenk seien massenlos. Die Aufhängung geschieht aus Gleichgewichtsgründen in der Mitte des Joches.

Abb. 1: Zwei Massen

Nun kombinieren wir diese Startfigur mit einem weiteren Joch und einer weiteren, ebenso großen Masse (Abb. 2). Der Aufhängepunkt am zweiten Joch ist nun nach dem ersten Drittel.

Abb. 2: Zwei Joche und drei Massen

Beim dritten Joch ist der Aufhängepunkt nach dem ersten Viertel (Abb. 3).

Abb. 3: Drei Joche

Wir sehen, wie es weitergeht (Abb. 4).

Abb. 4: Aufhängung des Mobile

4 Exponentialkurve

In den Abbildungen 5 und 6 ist zusätzliche eine Exponentialkurve eingezeichnet. Sie approximiert den visuellen Verlauf des Mobile.

Abb. 5: Exponentialkurve

Abb. 6: Exponentialkurve

Hintergrund: Die Figur wächst in der x-Richtung wie die harmonische Riehe, in der y-Richtung linear. Wir approximieren die harmonische Reihe durch das Integral:

Die approximierende Wachstumskurve ist also eine auf die y-Richtung bezogene Logarithmuskurve. Auf die x-Richtung bezogen ist das eine Exponentialkurve.

Verwendete Daten: Die Joche haben die Länge 1, der Höhenabstand zwischen zwei Jochen ist h = 0.25 . Die Exponentialkurve hat die Gleichung y = h exp(x) .

5 Aufbauen statt Aufhängen

Aus Quadern bauen wir eine Treppe. Die folgenden Abbildungen zeigen die Situation von der Seite.

Wir beginnen mit einem Quader (Abb. 7).

Abb. 7: Startquader

Nun heben wir den ersten Quader um eine Quaderhöhe an und schieben den zweiten Quader von rechts her darunter bis in die Mitte (Abb. 8). Der erste Quader liegt jetzt auf dem zweiten Quader, allerdings in einem sehr labilen Gleichgewicht. Wenn wir aber die Länge der Quader um eine beliebig kleine positive Zahl vergrößern („epsilon“ im mathematischen Jargon), ergibt sich ein stabiles Gleichgewicht.

Abb. 8: Zweiter Quader unter dem ersten

Nun heben wir wieder an und schieben den dritten Quader darunter (Abb. 9). Um die Gleichgewichtslage zu erhalten, müssen wir bis zum vorderen Drittel des zweiten Quaders vorschieben.

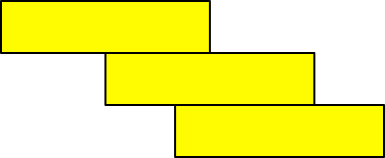
Abb. 9: Dritter Quader

Wir sehen, wie es weitergeht (Abb. 10).

Abb. 10: Bau der Treppe

Der Aufbau erfolgt nicht additiv von unten nach oben, sondern es wird bei jedem Schritt die bisherige Treppe um eine Stufenhöhe angehoben und die neue Stufe darunter geschoben. Wollte man additiv von unten nach oben bauen, müsste man vor Baubeginn die Anzahl der Stufen festlegen. Damit käme man beim Turmbau zu Babel in Schwierigkeiten.

Durch Symmetrisieren erhalten wir ein Tor, das aus vorkragenden Quadern aufgebaut ist (Abb. 11).

Abb. 11: Torbau