Hans Walser, [20110228a]
Herzkurve
1
Worum geht es
Ein Algorithmus zur Konstruktion des Eckenschwerpunktes von regelmŠ§igen Vielecken fŸhr zu einer Herzkurve. Es handelt sich dabei nicht um die Kardioide.
2 Eckenschwerpunkt eines n-Eckes
Die Abbildung 1 illustriert
einen Algorithmus zur Konstruktion des Eckenschwerpunktes am Beispiel des
regelmŠ§igen FŸnfecks. Das Verfahren funktioniert analog fŸr irgend ein
Vieleck, es braucht nicht regelmŠ§ig zu sein.
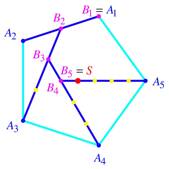
Abb. 1: Eckenschwerpunkt
Wir beginnen mit der
Ecke 
und setzen 
. Dann sei 
der Mittelpunkt
der Strecke 
. Den Punkt 
konstruieren wir
so, dass er die Strecke 
im VerhŠltnis
1:2 teilt. Das TeilverhŠltnis ist durch einen gelben Punkt angedeutet.
Allgemein sei nun 
derjenige Punkt,
der die Strecke 
im VerhŠltnis 
teilt. Auf Grund
der Hebelgesetze ist 
der Schwerpunkt
der Punkte 
, also der ersten j
Punkte. Der Punkt 
ist dann der
Schwerpunkt S sŠmtlicher n Punkte.
3
Zwischenbemerkung
Dieses schrittweise
Konstruieren des Schwerpunktes scheint etwas mŸhsam, vor allem, wenn man
bedenkt, dass der rechnerische Weg Ÿber die Koordinatendurchschnitte auf Anhieb
und unabhŠngig von der Eckenzahl funktioniert. Doch der Schein trŸgt: Bei der
Durchschnittsberechnung mŸssen wir zunŠchst die Zahlen addieren. Doch niemand
kann zum Beispiel fŸnf Zahlen auf einen Streich addieren. Der tatsŠchliche
Rechenweg geht etwa so:
Wir addieren zunŠchst
zwei Zahlern, zur Summe davon die dritte Zahl und so weiter. Das entspricht
genau unserem Konstruktionsalgorithmus.
4
Beispiele
Die Abbildung 2 zeigt
die Konstruktion fŸr regelmŠ§ige Vielecke mit den Eckenzahlen 
. Der
Schwerpunkt ist natŸrlich der Mittelpunkt. Ohne die SchwerpunktŸberlegung wŠre
es aber nicht direkt einsehbar, dass es zum Beispiel beim Quadrat mit den
VerhŠltnissen so schšn aufgeht.
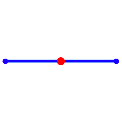
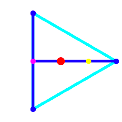
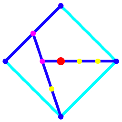
Abb. 2: Beispiele
Die Abbildung 3 zeigt
das regelmŠ§ige 16-Eck, die Abbildung 4 das 32-Eck.
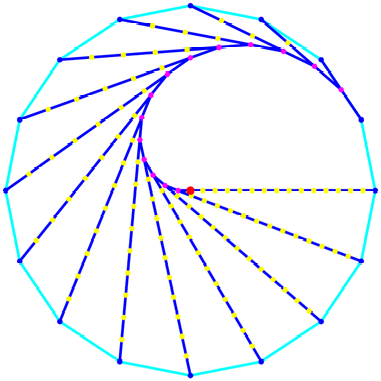
Abb. 3: 16-Eck
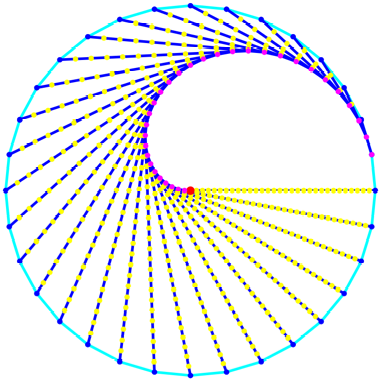
Abb. 4: 32-Eck
Im Lichtraum zeigt sich
eine halbe Herzkurve. Was fŸr eine Kurve ist das?
5
Schwerpunkt eines Kreisbogens
FŸr 
ergibt sich aus
den regelmŠ§igen Vielecken als Grenzfigur der Kreis. Da die magenta Punkte
jeweils Schwerpunkte der ersten Ecken dies Vieleckes sind, ergeben sich die
Punkte der Herzkurve als Schwerpunkte von Kreisbšgen.
Im folgenden arbeiten
wir im Einheitskreis.
Wir berechnen den
Ortsvektor 
des
Schwerpunktes des Kreisbogens:
Dieser Bogen hat die
LŠnge T. FŸr den Bogenschwerpunkt 
muss gelten:
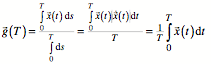
Dabei ist das
Bogenelement 
und wegen 
ist 
. FŸr das Integral erhalten wir:
Somit ist:
Das lŠsst sich noch
etwas umformen, um eine schšne Polarform zu erhalten. Mit der Substitution 
erhalten wir:
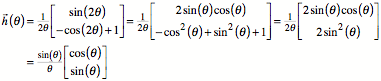
Wegen 
ist 
.
6
Die Herzkurve
Die halbe Herzkurve
wird also beschrieben durch:
Die Abbildung 5 zeigt
das 32-Eck der Abbildung 4 zusammen mit der halben Herzkurve als Grenzkurve.
Die Approximation ist schon recht gut.
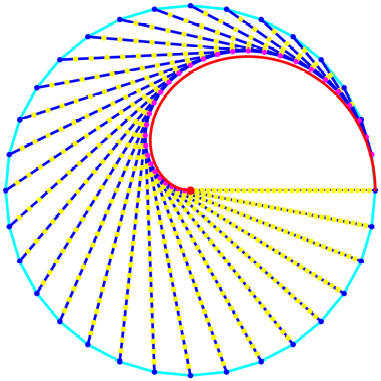
Abb. 5: Halbe Herzkurve
FŸr 
ergibt sich die
ganze Herzkurve. In der Abbildung 6 ist im Einheitskreis in rot die ganze
Herzkurve eingezeichnet, zusŠtzlich in grŸn die Kardioide. Offensichtlich ist
unsere Herzkurve nicht die Kardioide.
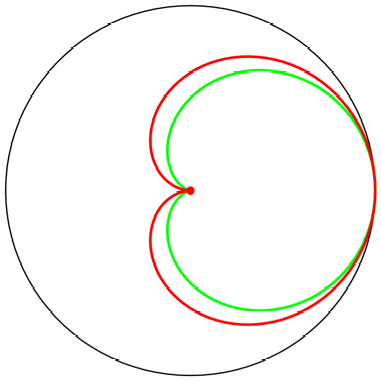
Abb. 6: Herzkurve und
Kardioide
Die Abbildung 7 zeigt
das Herz.
Abb. 7: Rotes Herz