Hans Walser, [20150729]

Herzkurve

1 Worum geht es?

Es werden Variationen zur Herzkurve vorgestellt. Geometrische Spielerei ohne mathematischen Gehalt.

2 Klassische Herzkurve

Die Abbildung 1 zeigt die klassische Herzkurve. Die Darstellung ist so gewählt, dass die Symmetrieachse senkrecht steht.

Abb. 1: Herzkurve

Die Kurve wurde mit folgendem Programm gezeichnet (die gelbe Farbe wurde nachträglich eingefügt):

with(plots): with(plottools):

p:=0: # Parameter1

q:=0: # Parameter2

R:=1: # Radius Trägerkreis

r:=0.5: # Radius abgedrehter Kreis

Kurve:=plot([R*sin(t)*abs(sin(t))^(p) + r*sin(2*t)*abs(sin(2*t))^(q), -(R*cos(t)*abs(cos(t))^(p) + r*cos(2*t)*abs(cos(2*t))^(q)), t=0..2*Pi], thickness=1, color=red):

display([Kurve], scaling=constrained , axes=none);

Das ist ein bisschen viel Holz für eine Geige. Man kann sich die Bedeutung der mit p und q versehenen Normierungsfaktoren überlegen.

3 Varianten

Wir schrauben nun an den Parametern p und q schauen was geschieht. Im Folgenden einige wenige Beispiele.

3.1 p = 0

Zunächst setzen wir p = 0.

Abb. 2.1: q = –1

Abb. 2.2: q = – 0.5

Abb. 2.3: q = 0.5

Abb. 2.4: q = 1

Abb. 2.5: q = 2

Abb. 2.6: q = 10

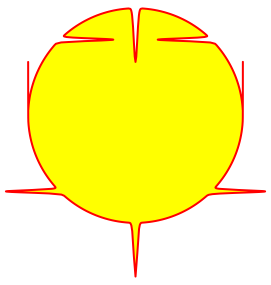
Abb. 2.7: q = 1000

3.2 q = 0

Nun wählen wir q = 0.

Abb. 3.1: p = – 1

Abb. 3.2: p = – 0.5

Abb. 3.3: p = 0.5

Abb. 3.4: p = 1

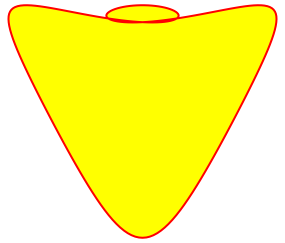
Abb. 3.5: p = 2

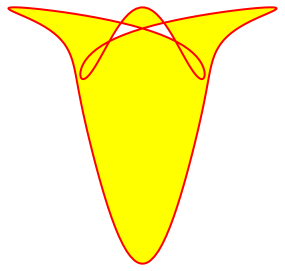
Abb. 3.6: p = 10

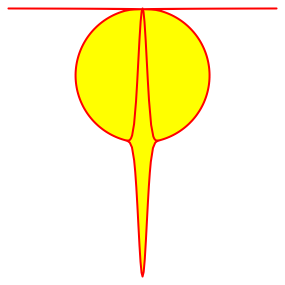
Abb. 3.7: p = 1000

3.3 p = q

Schließlich wählen wir p und q gleich groß.

Abb. 4.1: p = q = – 1

Abb. 4.2: p = q = – 0.5

Abb. 4.3: p = q = 0.5

Abb. 4.4: p = q = 1

Abb. 4.5: p = q = 2

Abb. 4.6: p = q = 10

Abb. 4.7: p = q = 1000