Hans Walser, [20151122]

Herzkurve

Idee und Anregung: R. Sch., C.

1 Worum geht es?

Es werden zwei Methoden vorgestellt, die Herzkurve zu gewinnen.

2 Enveloppe

2.1 Vorgehen

Wir wählen einen beliebigen Winkel und definieren die Punktefolge:

(1)

Für praktische Zwecke muss man natürlich für n eine Obergrenze N festlegen.

Das Polygon hüllt die Herzkurve ein.

Die Abbildung 1a zeigt die Situation für und , bei der Abbildung 1b wurde der Winkel gleich belassen, aber gewählt.

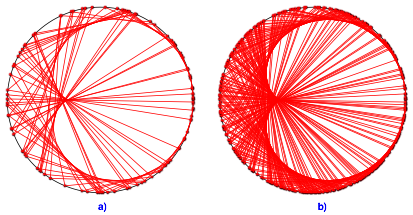
Abb. 1: Herzkurve als Enveloppe

2.2 Probleme

So ganz beliebig darf nicht gewählt werden.

2.2.1 Zyklen

Für und erhalten wir die nicht sehr umwerfende Figur der Abbildung 2.

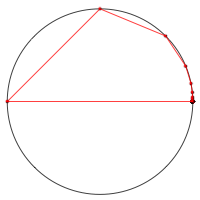
Abb. 2: Wo ist die Herzkurve?

2.2.2 Auslöschung?

Für und erhalten wir die etwas verschwommene Figur der Abbildung 3.

Abb. 3: Verschwommene Figur

Ich vermute, dass Auslöschungseffekte daran schuld sind.

3 Drittelpunkte

3.1 Vorgehen

Auf der Strecke bezeichnen wir mit den näher bei liegenden Drittelpunkt. Und nun zeichnen wir lediglich diese Drittelpunkte. Die Abbildung 4a zeigt die Situation für und . In der Abbildung 4b wurde gewählt.

Abb. 4: Drittelpunkte

Die Punkte liegen allerdings nicht optisch aufeinanderfolgend. Die Abbildung 5a zeigt Das Polygon für und . In der Abbildung 5b wurde gewählt.

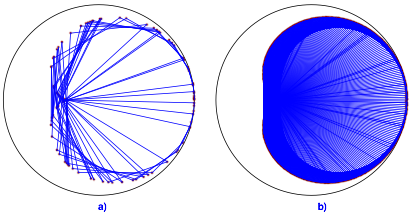
Abb. 5: Polygonzug

3.2 Ausreißer

Die Abbildung 6 zeigt die Punkte für und . Wir haben offensichtliche Ausreißer.

Abb. 6: Ausreißer

3.3 Verallgemeinerung

Anstelle von (1) definieren wir die Punktfolge:

(2)

Die Basis 2 wird durch die allgemeine Basis b ersetzt.

Auf der Strecke bezeichnen wir mit nun den näher bei liegenden ersten Teilpunkt bei Unterteilung in gleiche Teile.

Die Abbildung 7 zeigt die Situation für , und .

Abb. 7: Sechspass