Hans Walser, [20190703]

Herzkurve

1 Worum geht es?

Durch gleichmäßige Krümmung einer Strecke erhalten wir eine Herzkurve. Allerdings handelt es sich nicht um die Kardioide.

2 Vorgehen

2.1 Strecke

Wir zeichnen eine senkrechte Strecke (Abb. 1).

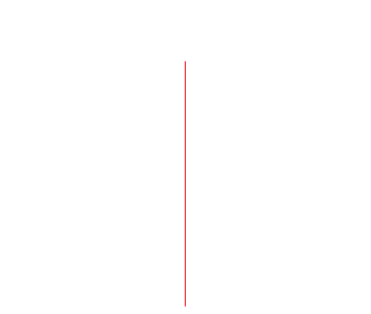
Abb.1: Senkrechte Strecke

2.2 Kreisbögen

Nun zeichnen wir Kreisbögen gleicher Länge, aber unterschiedlicher Krümmung. Die Kreisbögen sollen die Strecke im Anfangspunkt oben berühren. Die Abbildung 2 zeigt zwei Beispiele.

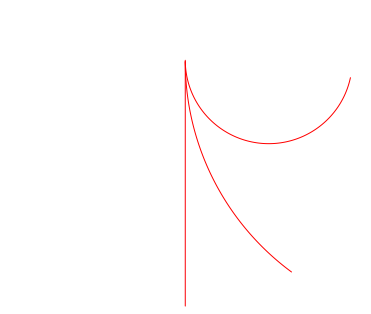
Abb. 2: Kreisbögen

Wir krümmen so lange und auf beide Seiten, bis sich die Bögen zum Kreis schließen (Abb. 3).

Abb. 3: Krümmen bis zum Kreis

2.3 Umrisskurve

Die Umrisskurve der Figur ist eine Herzkurve (Abb. 4).

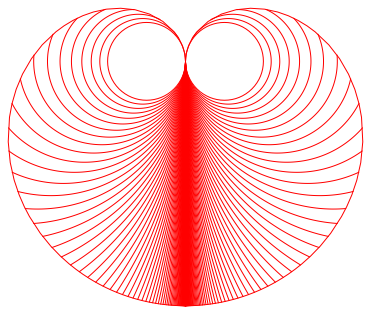
Abb. 4: Herzkurve

Der rechte Teil der Herzkurve etwa kann beschrieben werden durch:

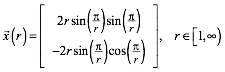(1)

Die Herzkurve kann auch eleganter beschrieben werden durch:

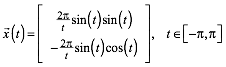(2)

2.4 Vergleich mit Kardioide

In der Abbildung 5 ist zusätzlich die Kardioide (blau) eingepasst. Unsere Herzkurve ist nicht die Kardioide.

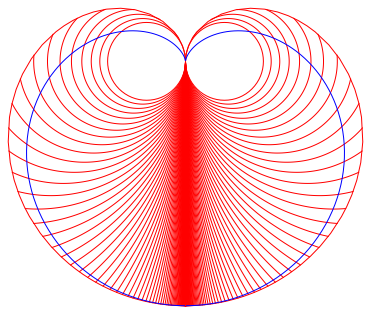
Abb. 5: Vergleich mit Kardioide

Websites

[1] Hans Walser: Herzkurve

http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve/Herzkurve.htm

[2] Hans Walser: Herzkurve

http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve2/Herzkurve2.htm

[3] Hans Walser: Herzkurve

http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve3/Herzkurve3.htm

[4] Hans Walser: Herzkurve

http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve5/Herzkurve5.htm

[5] Hans Walser: Die Herzkurve und die Möndchen des Hippokrates

www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve_u_Hippokrates/Herzkurve_u_Hippokrates.htm

[6] Hans Walser: Herzkurven

http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurven/Herzkurven.htm