Hans Walser, [20190728]
Herzkurve
1 Worum geht es?
KreisŸberlagerungen fŸhren zu einer Herzkurve. Es handelt sich nicht um die Ÿbliche Kardioide, sondern um die in [4] beschriebene Herzkurve.
2 KreisŸberlagerungen
Wir arbeiten mit der Figurenfolge
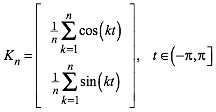(1)
Es handelt sich dabei um eine †berlagerung von n Kreisen. Die Abbildungen 1 geben die Beispiele fŸr n = 1, ... ,5.
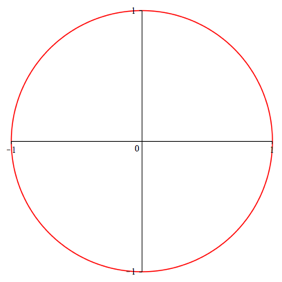
Abb. 1.1 n = 1, Kreis
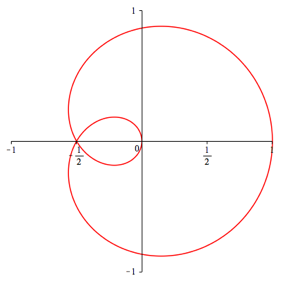
Abb. 1.2: n = 2
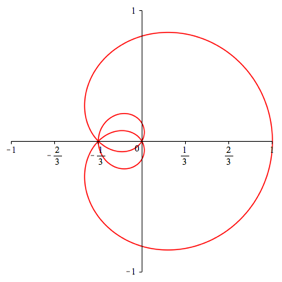
Abb. 1.3: n = 3
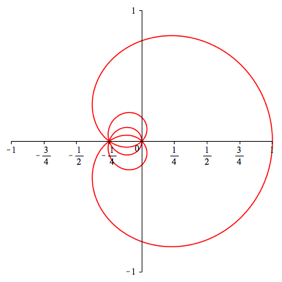
Abb. 1.4: n = 4
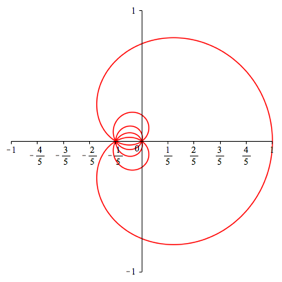
Abb. 1.5: n = 5
Auf Grund der Beispiele vermuten wir:
Die Kurve
verlŠuft n Mal durch den Punkt 
und n – 1 Mal durch den Ursprung. FŸr t = 0 verlŠuft sie durch den Punkt 
.
3 Parameterwerte der Mehrfachpunkte
Die Parameterwerte der Mehrfachpunkte ergeben sich durch:
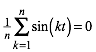(2)
Wir suchen also die Nullstellen der Funktion:
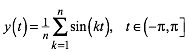(3)
Die Abbildungen 2 geben in rot die Funktionsgrafen fŸr n = 1, ... , 5. In blau sind die Funktionsgrafen von
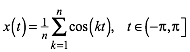(4)
eingetragen
und in grŸn die Linie auf dem Niveau 
.
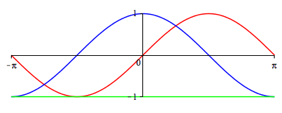
Abb. 2.1: n = 1, Sinuskurve
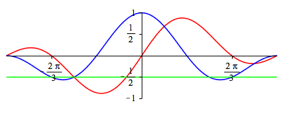
Abb. 2.2: n = 2
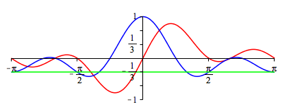
Abb. 2.3: n = 3
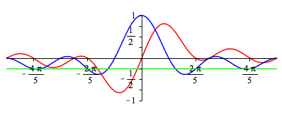
Abb. 2.4: n = 4
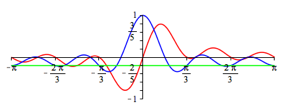
Abb. 2.5: n = 5
Aus den Funktionsgrafen lesen wir zunŠchst die Nullstellen
(5)
ab. Diese Nullstellen sind trivial, wie am Einheitskreis Ÿberlegt werden kann. Weiter ist an diesen Stellen
(6)
Dies kann
ebenfalls am Einheitskreis Ÿberlegt werden (die ãEinsÒ fehlt). Dieser Sachverhalt
wird auch in den Abbildung 2 illustriert. Somit gehšren mit Ausnahme von t = 0 diese Nullstellen als Parameterwerte
der Kurve zum Punkt 
.
Spannend sind nun die anderen Nullstellen. Diese gehšren als Parameterwerte der Kurve zum Ursprung. Wir haben das Gleichungssystem
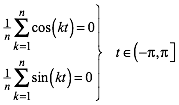(7)
zu lšsen (vgl. dazu die Abbildungen 2.2 bis 2.5). Wir erhalten die Lšsungen:
(8)
Dies kann ebenfalls am Einheitskreis eingesehen werden. Die Abbildungen 3 illustrieren den Sachverhalt.
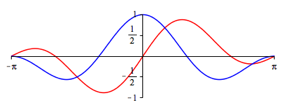
Abb. 3.2: n = 2
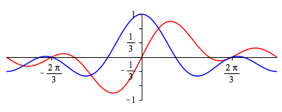
Abb. 3.3: n = 3
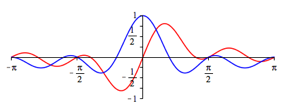
Abb. 3.4: n = 4
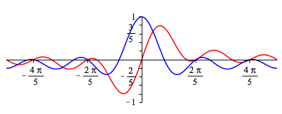
Abb. 3.5: n = 5
4 Und nun die Herzkurve
FŸr 
nŠhern
sich die Kurven der Abbildungen 1 (bis auf einen Skalierungsfaktor) der
Herzkurve von [4]
an. Diese kann dargestellt werden in der Form:
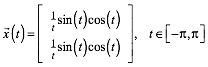(9)
Die
Abbildung 4 zeigt zwei Beispiele. In Blau ist die Herzkurve von [4]
eingetragen.
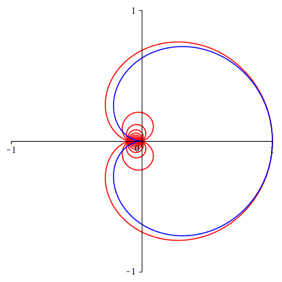
Abb.
4.1: n = 10
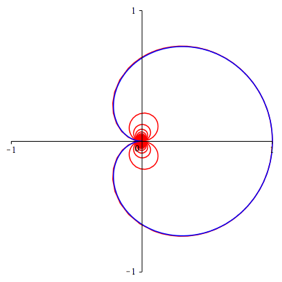
Abb.
4.2: n = 100
Die Abbildung 5 zeigt das Herz (fŸr n =100) in der Ÿblichen Darstellung.
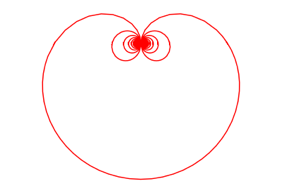
Abb. 5: Herzkurve
Websites
[1] Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve/Herzkurve.htm
[2] Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve2/Herzkurve2.htm
[3] Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve3/Herzkurve3.htm
[4] Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve4/Herzkurve4.htm
[5] Hans Walser: Die Herzkurve und die Mšndchen des Hippokrates
www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve_u_Hippokrates/Herzkurve_u_Hippokrates.htm
[6] Hans Walser: Herzkurven
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurven/Herzkurven.htm