Hans Walser, [20130429a]
Die Herzkurve und die Mšndchen des Hippokrates
1 Parameterdarstellung der Herzkurve
Die Kardioide entsteht durch Abrollen des gelben Kreises auf dem grźnen (Abb. 1).
(1)
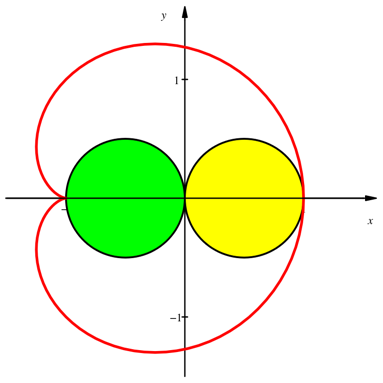
Abb. 1: Kardioide
2 Extrempunkte
2.1 Hoch- und Tiefpunkte
Aus
(2)
ergibt sich 
. Dies fźhrt zu den Punkten:
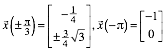(3)
2.2 Links- und Rechtspunkte
Aus
(4)
ergibt sich 
. Dies fźhrt zu den Punkten:
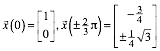(5)
Die Extrempunkte liegen
auf einem Dreiecksraster (Abb. 2). Sie gehšren der Reihe nach zu den
Parameterwerten 
.
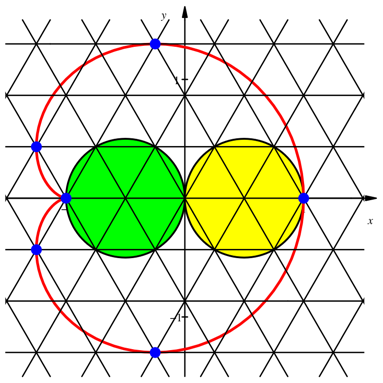
Abb. 2: Extrempunkte
3 BogenlŠngen
3.1 Gesamte BogenlŠnge
Es ist:
(6)
Damit wird:
(7)
Mit der Substitution 
erhalten wir:
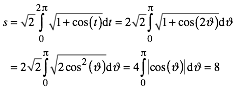(8)
Bemerkenswert ist das ganzzahlige Resultat.
3.2 BogenlŠngen zwischen den Extrempunkten
Wir berechnen die in der Abbildung 3 eingezeichneten BogenlŠngen a, b und c.
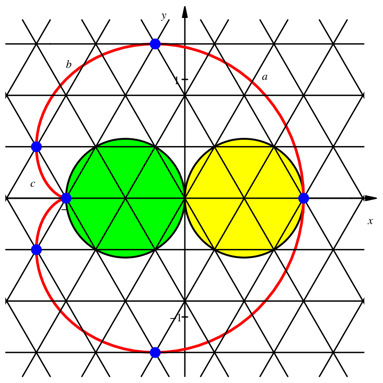
Abb. 3: BogenlŠngen
Wir erhalten:
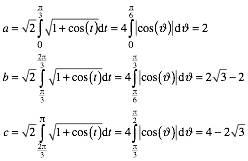(9)
Vor allem die BogenlŠnge von a ist bemerkenswert. Es ist ein Viertel der gesamten BogenlŠnge.
4 Quadratraster
Im Quadratraster finden
wir 4 Rasterpunkte auf der Kardioide (Abb. 4). Diese gehšren zu den
Parameterwerten 
.
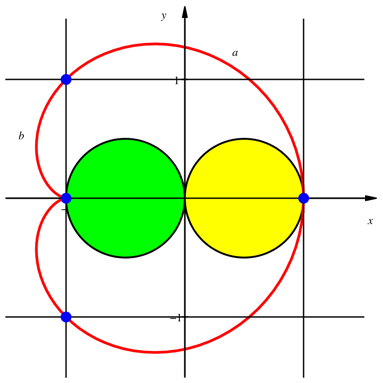
Abb. 4: Im Quadratraster
Fźr die eingezeichneten BogenlŠngen erhalten wir:
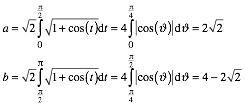(10)
Weiter ist:
(11)
Wir haben also
Steigungswinkel von 
.
5 Die Mšndchen des Hippokrates
5.1 Der Klassiker
Die Abbildung 5 zeigt einen Klassiker der Schulgeometrie (vgl. [Heinrich / Schmitz / Walser 1999]).
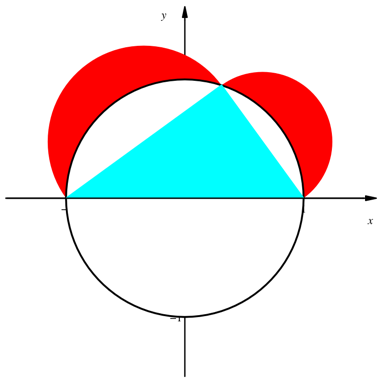
Abb. 5: Die Mšndchen des Hippokrates: Rot = Cyan
Die Mšndchen sind durch den Thaleskreis des rechtwinkligen Dreiecks innen und durch Thaleskreise źber den Katheten au§en berandet. Die Summe der MšndchenflŠchen ist gleich gro§ wie die DreiecksflŠche.
Fźr die folgenden Feststellungen fehlen mir die Beweise.
5.2 Die Kardioide
Das Mšndchen links berźhrt unsere Kardioide (Abb. 6).
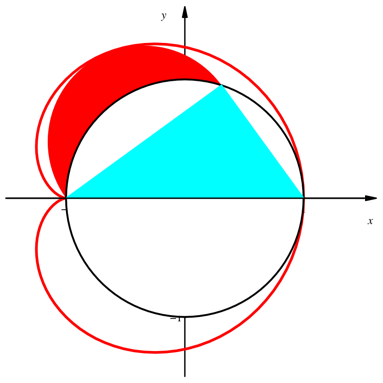
Abb. 6: Mšndchen und Kardioide
Entsprechend berźhrt das andere Mšndchen die gespiegelte Kardioide (Abb. 7).
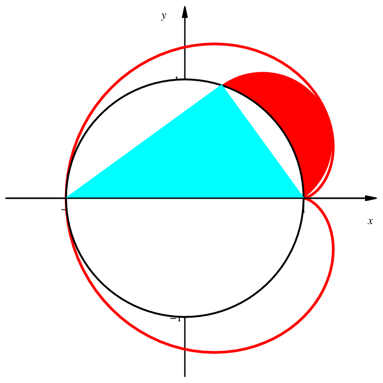
Abb. 7: Gespiegelte Kardioide
Die Kardioide ist die Enveloppe der auf den Katheten aufgesetzten Thaleskreise (Abb. 8).
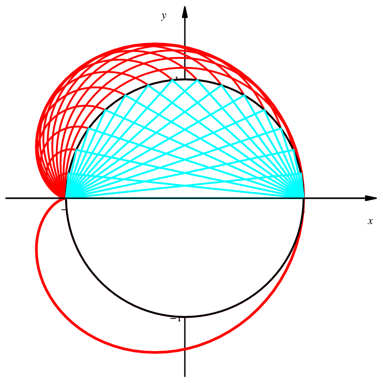
Abb. 8: Enveloppe
5.3 SonderfŠlle
In einem rechtwinkligen Dreieck mit Winkeln von 30ˇ und 60ˇ berźhren die Mšndchen Extrempunkte der Kardioiden (Abb. 9).
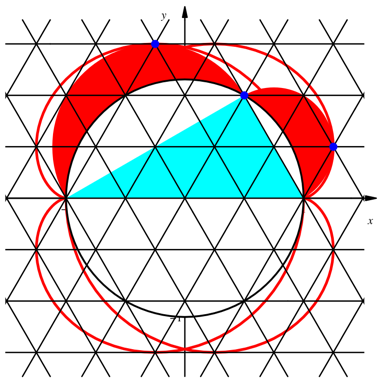
Abb. 9: Sonderfall 30ˇ und 60ˇ
Im rechtwinklig gleichschenkligen Dreieck passt die Sache in den Quadratraster (Abb. 10).
Abb. 10: Sonderfall rechtwinklig gleichschenkliges Dreieck
Literatur
[Heinrich / Schmitz / Walser 1999] Heinrich, Frank / Michael Schmitz / Hans Walser: Verallgemeinerungen der ÓMšndchen des HippokratesÓ. MNU Der mathematische und naturwissenschaftliche Unterricht 52/5, 1999, 264-270.