Hans Walser, [20210825]
Hexagonalfärbung
Anregung: Szilassi-Polyeder
1 Problemstellung
Wie kann ein Hexagonalraster (Sechseckraster, Bienenwabenmuster, Abb. 1) so mit sieben Farben gefärbt werden, dass jeweils jedes Sechseck umgeben ist von Sechsecken mit den sechs anderen Farben?

Abb. 1: Hexagonalraster
2 Lösung

Abb. 2: Eine Lösung
Gleichfarbige Sechsecke bilden ein Dreiecksraster.
3 Parkettstein
Aus dem Parkett der Abbildung 2 schneiden wir einen Rhombus heraus (Abb. 3). Seine Ecken sind die Mittelpunkt von vier gleichfarbigen Hexaedern.
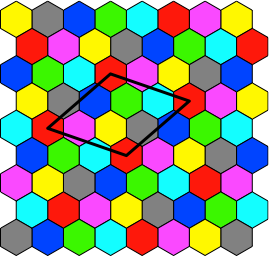
Abb. 3: Rhombus
Die Abbildung 4a zeigt diesen Rhombus separat. Er ist der minimale Parkettstein, mit dem das Parkett inklusive Färbung erzeugt werden kann. Fünf der sieben Hexaeder sind angeschnitten, aber der fehlende Teil kommt jeweils an der gegenüberliegenden Seite vor. Daher sind die Flächenanteile aller sieben Farben gleich.
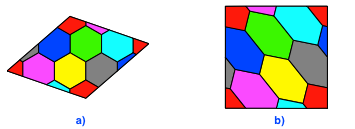
Abb. 4: Parkettstein
Wir deformieren den Rhombus zum Quadrat (Abb. 4b). Damit können ebenfalls Parkette mit gleichen Flächenanteilen der sieben Farben ausgelegt werden (Abb. 5).

Abb. 5: Parkett mit gleichen Farbanteilen
4 Torus
Wir
identifizieren im quadratischen Parkettstein gegenüberliegende Seiten (Abb. 6).
Dadurch erhalten wir einen Torus mit einer Unterteilung in sieben Sechsecke
(auf dem Torus sind sie nicht mehr kongruent) so dass jedes Sechseck mit jedem
der sechs anderen eine Kante gemeinsam hat. Das ist auch die Topologie des Szilassi-Polyeders.
Vorgehen: Zuerst die beiden orangen Kanten identifizieren. So entsteht ein Zylinder. Dieser Schritt ist mit einem auf Papier ausgedruckten Parkettstein verzerrungsfrei machbar. Dann den Zylinder zu einem gebogenen Rohr verbiegen, bis die violetten Enden aneinanderstoßen. Dieser Schritt ist mit Papier nicht mehr machbar.

Abb. 6: Torus
Die Abbildung 7 ist eine Modifikation der Abbildung 6.

Abb. 7: Modifikation
Diese
Figur ist weitgehend „orthogonalisiert“. Die
Eckpunkte liegen alle auf einem ![]() -Quadratgitter (Abb. 8). Das erleichtert die Programmierarbeit für die
3d-Darstellungen.
-Quadratgitter (Abb. 8). Das erleichtert die Programmierarbeit für die
3d-Darstellungen.
Die Zahl sieben lässt uns nicht los.
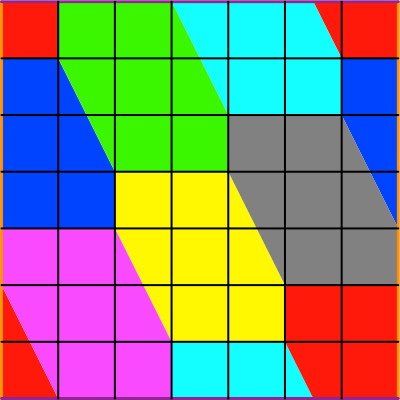
Abb. 8: Quadratgitter
Die Abbildungen 9 und 10 zeigen die Situation auf dem Torus.

Abb. 9: Donut
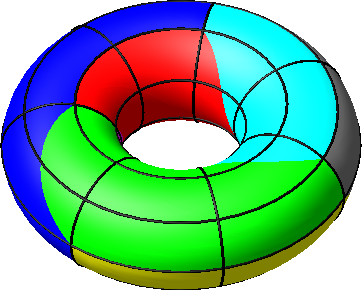
Abb. 10: Torus mit Netz
5 Drehen und Rollen
Die Abbildungen 11 und 12 zeigen die Drehung um die Rotationsachse des Torus.

Abb. 11: Drehung um Rotationsachse des Torus
Beim Drehen um die Rotationsachse des Torus sind die Breitenkreise globale Fixkreise (Abb. 12).
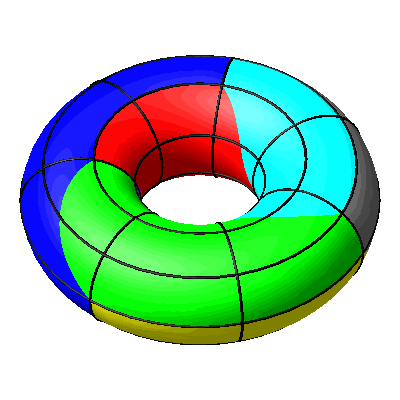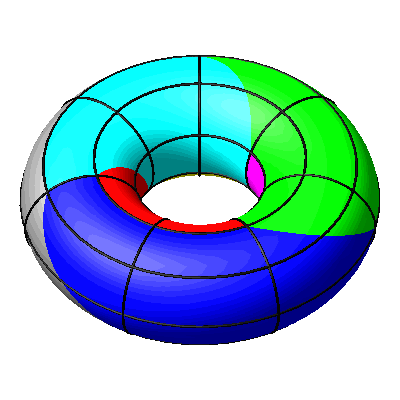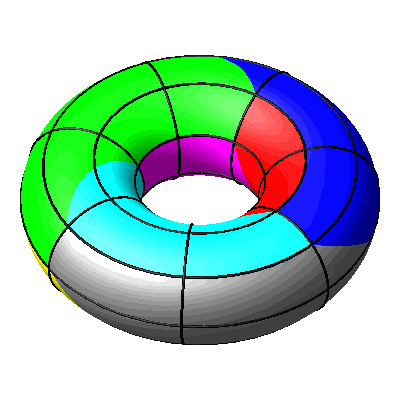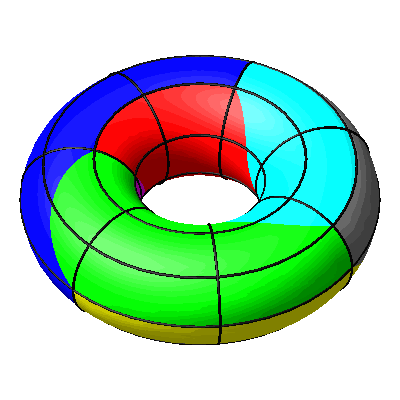
Abb. 12: Breitenkreise global fix
In den Abbildungen 13 und 14 wird der Torus eingerollt.

Abb.13: Einrollen
Beim Einrollen bleiben die Meridiane global fix.
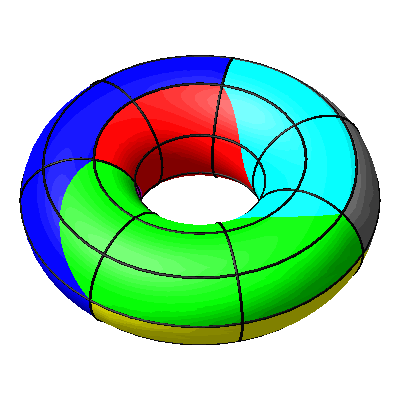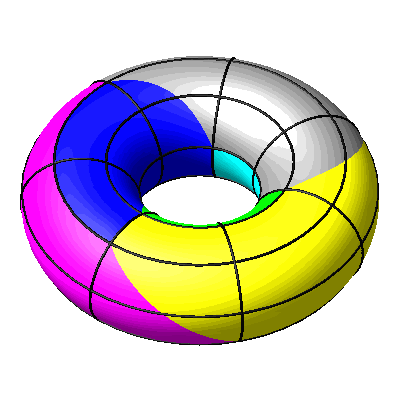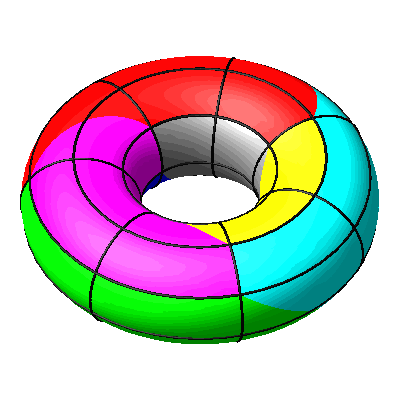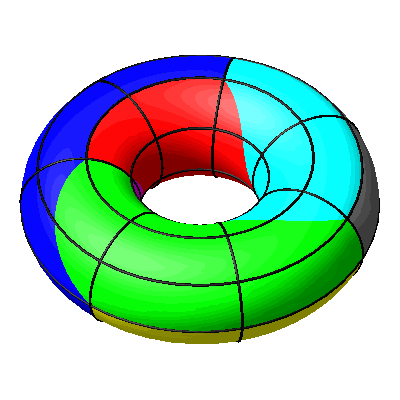
Abb. 14: Meridiane global fix
Drehen und Rollen können kombiniert werden (Abb. 15 und 16).

Abb. 15: Kombination
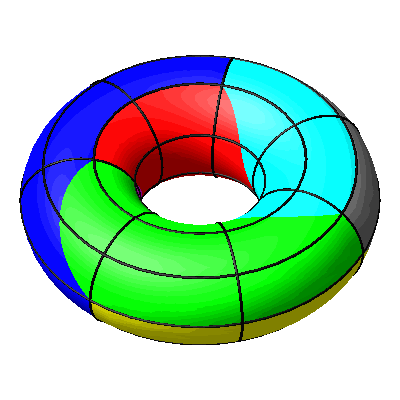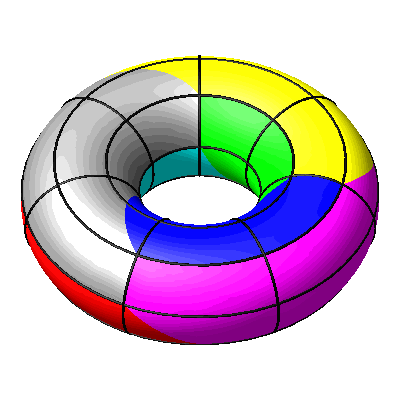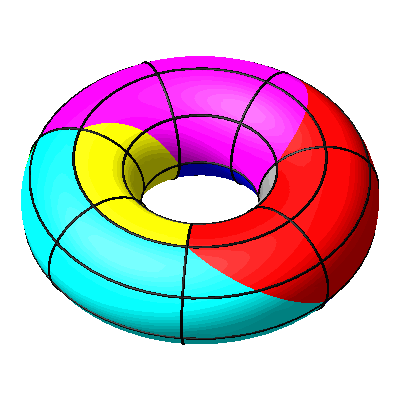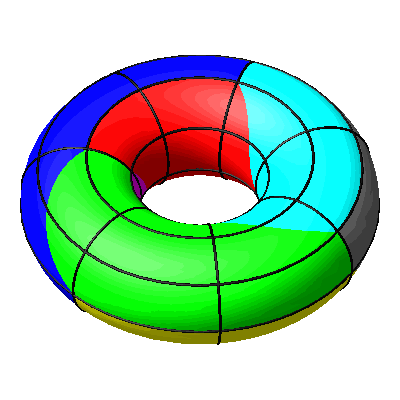
Abb. 16: Drehen und Rollen
Websites
Szilassi-Polyeder
https://de.wikipedia.org/wiki/Szilassi-Polyeder