Hans Walser, [20150606]

Hexenspirale

Anregung: (Kalman and Verdi, 2015)

1     Was ist eine Hexenspirale?

Eine Hexenspirale besteht aus zwei eckigen logarithmischen Spiralen, die sich wechselseitig ein- und umbeschrieben sind. Die Abbildung 1 zeigt ein Beispiel.

 

Abb. 1: Hexenspirale

 

2     Konstruktion

Es gibt zwei Mšglichkeiten. Wir kšnnen entweder vom grš§ten (roten) rechtwinkligen Dreieck ausgehen und den passenden Verkleinerungsfaktor fŸr den †bergang zu nŠchsten Dreieck suchen oder wir kšnnen den Verkleinerungsfaktor vorgeben und das passende Startdreieck suchen.

Wir arbeiten mit den Bezeichnungen der Abbildung 2.

 

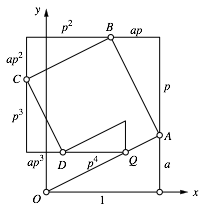
Abb. 2: Bezeichnungen

 

Das grš§te rechtwinklige Dreieck habe die Katheten 1 und a. Den Verkleinerungsfaktor bezeichnen wir mit p.

Im Koordinatensystem der Abbildung 2 gilt:

 

 

 

 

 

 

 

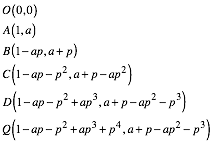
Die Schlie§ungsbedingung, also die Bedingung dass Q auf der Hypotenuse OA liegt, lautet:

 

 

 

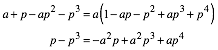
2.1    Verkleinerungsfaktor gesucht

Aus der Schlie§ungsbedingung erhalten wir bei gegebenem a fŸr den Verkleinerungsfaktor p:

 

 

Da die Lšsung  nicht interessant ist, bleibt fŸr p die kubische Gleichung:

 

 

2.2    Startdreieck gesucht

Zu gegebenem Verkleinerungsfaktor p suchen wir das passende a. Aus der Schlie§ungsbedingung erhalten wir die quadratische Gleichung fŸr a:

 

 

Diese quadratische Gleichung fŸr a hat positive reelle Lšsungen nur fŸr:

 

 

 

 

3     Beispiele

3.1    Startdreieck gegeben

FŸr  (rechtwinklig gleichschenkliges Dreieck) erhalten wir mit CAS die reelle Lšsung . Die Abbildung 3 zeigt die Spirale.

 

Abb. 3: Rechtwinklig gleichschenkliges Dreieck

 

FŸr  (DIN-Format, vgl. (Walser, 2015a) erhalten wir die reelle Lšsung  (Abb. 4).

 

Abb. 4: DIN-Format

 

FŸr  (goldener Schnitt, vgl. (Walser, 2013b)) erhalten wir die reelle Lšsung  (Abb. 5).

 

Abb. 5: Goldener Schnitt

 

3.2    Verkleinerungsfaktor gegeben

FŸr  ergeben sich fŸr a die beiden reziproken Lšsungen  und . Die zugehšrigen Startdreiecke haben dieselbe Form.

Die Abbildung 6 zeigt die Situation fŸr die erste Lšsung.

 

Abb. 6: Erste Lšsung

 

Die Abbildung 7 zeigt die Situation fŸr die zweite Lšsung. Die beiden Lšsungen sind spiegelbildlich.

 

Abb. 7: Zweite Lšsung

 

Literatur

Kalman, Dan and Verdi, Mark (2015): Polynomials with Closed Lill Paths. Mathematics Magazine, 88, 3-10.

Walser, Hans (2013a): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.

Walser, Hans (6. Auflage). (2013b). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.