Hans Walser, [20201015]

Hilfssatz 1

1 Worum geht es?

Ein Satz aus der Geometrie. Beweis rechnerisch mit CAS. Ein geometrischer Beweis ist mir nicht gelungen.

2 Schritt für Schritt

Abb. 1: Punkt auf Einheitskreis

Auf dem Einheitskreis zeichnen wir den festen Punkt A = (1, 0) und den variablen Punkt B = (cos(t), sin(t)) (Abb. 1).

Weiter zeichnen wir den von A ausgehenden Strahl c über B sowie dessen Spiegelbild d bei Spiegelung an der Geraden x = 1 (Abb. 2).

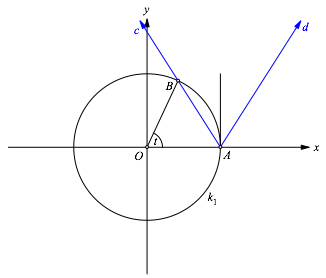
Abb. 2: Strahle

Die Strahle schneiden wir mit dem Kreis k₂ um den Ursprung und dem Radius . Die Schnittpunkte seien C und D (Abb. 3).

Abb. 3: Schnittpunkte

Der Punkt C hat die Koordinaten:

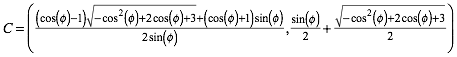
Für den Punkt D erhalten wir:

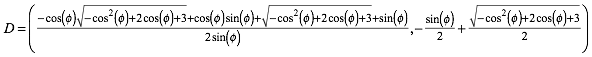
Nun zeichnen wir den Mittelpunkt M der Strecke CD (Abb. 4).

Abb. 4: Mittelpunkt

Dieser Mittelpunkt M hat die Koordinaten:

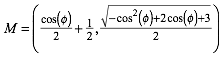
Wegen

liegt der Punkt M auf dem Kreis k₃ um A mit dem Radius 1 (Abb. 5).

Dies ist die Aussage des Hilfssatzes 1.

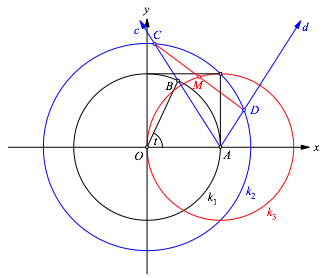
Abb. 5: Mittelpunkt auf Kreis