Hans Walser, [20130512a]

Hippokrates eckig

1 Worum es geht

Die Figur der Möndchen des Hippokrates wird verändert, indem die Halbkreise durch halbe regelmäßige Vielecke mit gerader Eckenzahl ersetzt werden. Die regelmäßigen Vielecke können dabei auf verschiedene Arten halbiert werden. Die Abbildung 1 zeigt die Situation für regelmäßige Sechsecke. Der „schiefe“ Fall der Abbildung 1b ist exemplarisch zu verstehen.

Abb. 1: Halbieren des Sechseckes

2 Halbieren längs einer Mittelpunkts-Diagonalen

Wir halbieren gemäß dem Beispiel der Abbildung 1a. Die Abbildung 2 zeigt die ersten Beispiele.

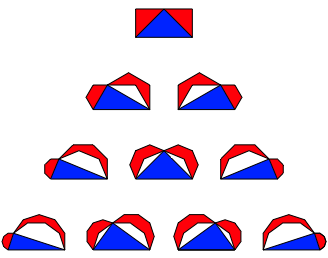
Abb. 2: Rot = Blau. Eckige Möndchen des Hippokrates

Der Nachweis der Flächengleichheit des blauen rechtwinkligen Dreiecks mit den beiden roten eckigen Möndchen verläuft analog zu dem der üblichen Möndchen des Hippokrates (Heinrich, F., Schmitz, M., Walser, H., 1999).

Da die Figuren aber Polygone sind, ist immer auch ein Zerlegungsbeweis möglich.

Die Abbildung 3 zeigt einen solchen Zerlegungsbeweis.

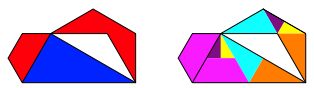
Abb. 3: Rot = Blau. Zerlegungsbeweis

3 Halbieren längs einer Symmetrieachse durch die Kantenmitten

Wir halbieren gemäß dem Beispiel der Abbildung 1c. Die Abbildung 4 zeigt die ersten Beispiele.

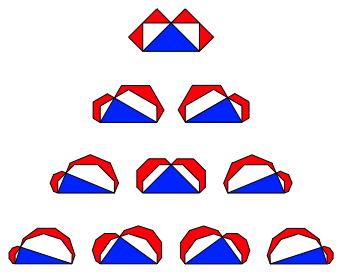
Abb. 4: Rot = Blau

4 Halbieren längs einer beliebigen Mittelpunkts-Geraden

Die Abbildung 5 zeigt „schiefe“ Beispiele gemäß Abbildung 1b.

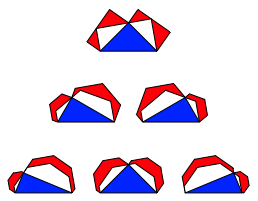
Abb. 5: Schiefe Beispiele

Literatur

Heinrich, F., Schmitz, M., Walser, H. (1999). Verallgemeinerungen der „Möndchen des Hippokrates“. MNU Der mathematische und naturwissenschaftliche Unterricht. 52(5), 264-270.