Hans Walser, [20230753]

Hochgoldenes Rechteck

1 Worum es geht

Ein Rechteck im Umfeld des Goldenen Schnittes

2 Das Hochgoldene Rechteck

Es sei Φ = (1+√5)/2 ≈ 1.618 der Goldene Schnitt.

Unter dem Hochgoldenen Rechteck (ad-hoc-Bezeichnung, man möge mir die überbordende Blumigkeit der Bezeichnung verzeihen) verstehen wir das Rechteck mit dem Seitenverhältnis Φ:(1/ Φ) (Abb. 1).

Abb. 1: Hochgoldenes Rechteck

3 Andere Schreibweisen des Seitenverhältnisses

Φ:(1/ Φ) = Φ²:1 = (1 + Φ):1 ≈ 2.618:1

Das Hochgoldene Rechteck ist also ziemlich lang.

4 Zugänge zum Hochgoldenen Rechteck

Unter dem (gewöhnlichen) Goldenen Rechteck verstehen wir das Rechteck mit dem Seitenverhältnis des Goldenen Schnittes, also Φ:1.

4.1 Ansetzen von Quadraten

Aus dem Goldenen Rechteck erhalten wir das Hochgoldene Rechteck wie folgt.

Wir können an einer Schmalseite des Goldenen Rechteckes ein Quadrat ansetzen (Abb. 2).

Abb. 2: Ansetzen eines Quadrates

Wir können an den beiden Längsseiten eines (hochkant stehenden) Goldenen Rechteckes je ein Quadrat ansetzen (Abb. 3).

Abb. 3: Ansetzen von zwei Quadraten

4.2 Rechtwinkliges Dreieck

Die Abbildung 4 zeigt eine Konstruktion mit einem rechtwinkligen Dreieck. Es hat das Kathetenverhältnis des Goldenen Schnittes, also Φ:1.

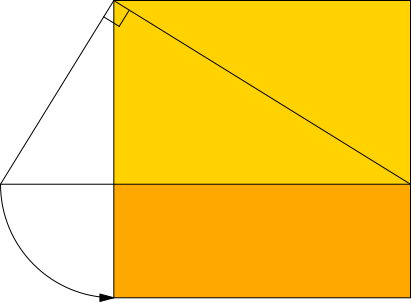
Abb. 4: Rechtwinkliges Dreieck

4.3 Unter der Hyperbel

Wir passen unter der Hyperbel y = 1/x ein Quadrat mit einer Ecke im Koordinatennullpunkt ein (hellblau in Abb. 5.1). Rechts daneben passen wir ein zweites Quadrat ein (gelb).

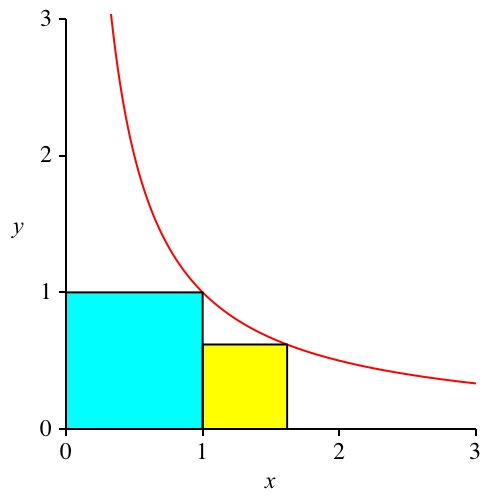
Abb. 5.1: Einpassen von Quadraten

Das achsenparallele Rechteck mit einer Ecke im Koordinatennullpunkt und der diametralen Ecke in der oberen rechten Ecke des zweiten (gelben) Quadrates ist ein Hochgoldenes Rechteck (Abb. 5.2).

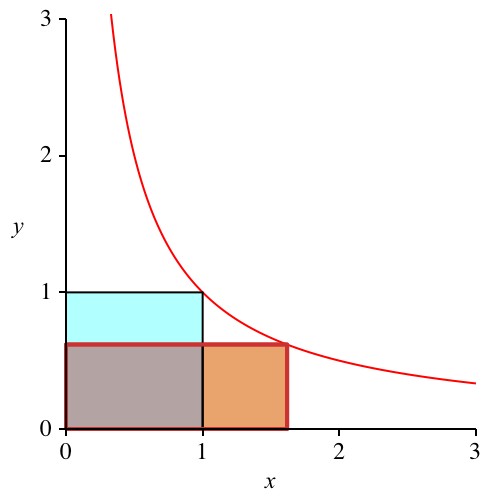
Abb. 5.2: Hochgoldenes Rechteck

4.4 Im Dodekaeder

Im regelmäßigen Dodekaeder finden wir Gerüste von drei paarweise orthogonalen Hochgoldenen Rechtecken (Abb. 6.1).

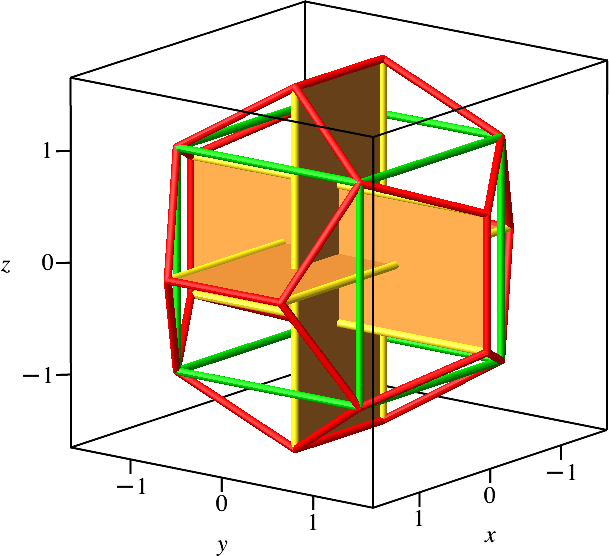
Abb. 6.1: Im Dodekaeder

Es gibt insgesamt fünf solcher Gerüste (Abb. 6.2). Somit gibt es im Dodekaeder insgesamt 15 Hochgoldene Rechtecke.

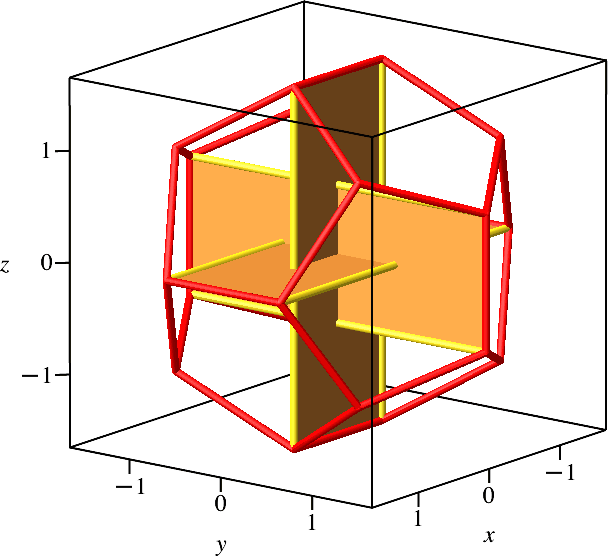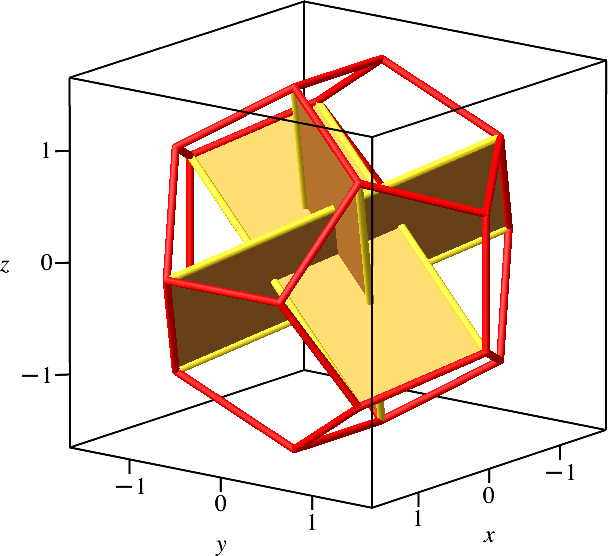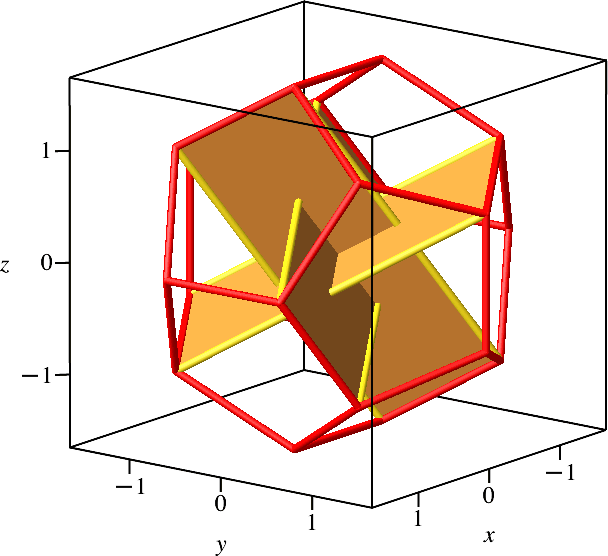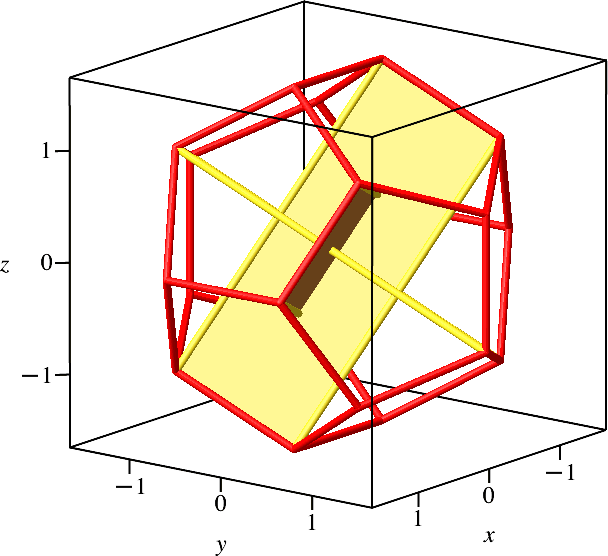
Abb. 6.2: Fünfzehn Gerüste im Dodekaeder

4.5 Hypotenusenabschnitte

Im rechtwinkligen Dreieck mit den Hpotenusenabschnitten Φ und 1/ Φ (Abb. 7) hat das aus diesen Abschnitten gebildete Hochgoldene Rechteck den Flächeninhalt 1, wie das Höhenquadrat (Höhensatz).

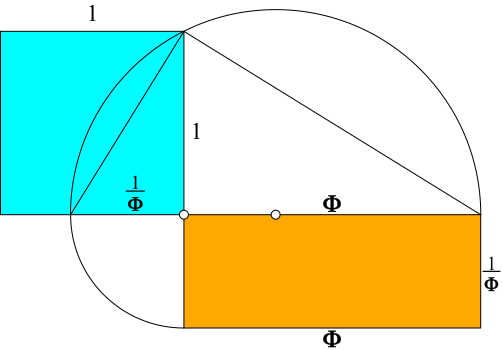
Abb. 7: Flächengleichheit

Wir versuchen, die Flächengleichheit durch gemeinsames Ausschöpfen zu zeigen. Wenn wir dies mit Goldenen Rechtecken (nun also gewöhnliche Goldene Rechtecke, in den Abbildungen 8 und 9 golden und grün gezeichnet) versuchen, bleibt nach dem ersten Schritt eine Figur übrig (grau), welche wiederum aus einem Hochgoldenen Rechteck und einem Quadrat besteht.

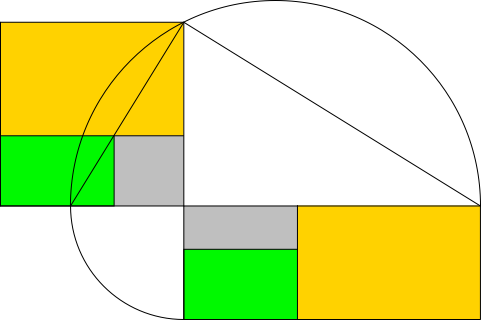
Abb. 8: Erster Ausschöpfungsschritt

Wir sind also sozusagen zurück auf Platz eins und können das Verfahren ad infinitum (in alle Ewigkeit) fortsetzen (Abb. 9).

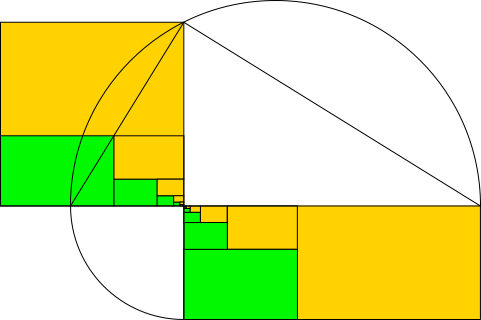
Abb. 9: Endloses Ausschöpfen

Es geht allerdings einfacher. Die Abbildung 10 zeigt eine gemeinsame Zerlegung, welche mit nur vier Teilen auskommt, von denen erst noch zwei und zwei kongruent sind. Allerdings müssen wir mit schrägen Linien arbeiten.

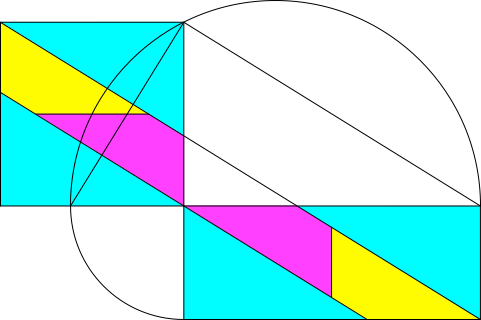
Abb. 10: Gemeinsame Zerlegung

Weblink

Hans Walser: Miniaturen: Goldener Schnitt

http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html