Hans Walser, [20230521]

Höhenabschnitte

Anregung: Hans Humenberger, Wien

1 Problemstellung

Ein Dreieck ABC habe den Höhenschnittpunkt H und die Höhenabschnitte (von H zu den Ecken) AH, BH, CH.

Gegeben seien die Höhenabschnitte, gesucht ist das Dreieck.

2 Rechnerische Lösung

Aus den Eckpunktkoordinaten A = [xA, yA], B = [xB, yB], C = [xC, yC] lässt sich H = [xH, yH] berechnen über:

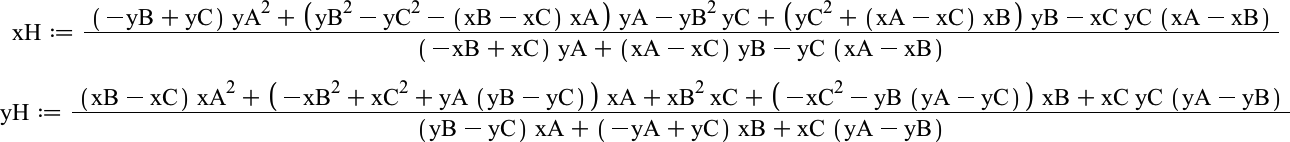
Die Distanz(P,Q) zwischen zwei Punkten P und Q berechnen wir wie üblich mit dem Pythagoras.

Wir setzen nun H in den Ursprung und C auf die positive y-Achse, also H = [0, 0] und C = [0, CH].

Dann lösen wir das Gleichungssystem

Distanz(A,H) = AH,
Distanz(B,H) = BH,
xH = 0,
yH = 0

nach xA, yA, xB, yB auf.

3 Programm (Maple)

Exemplarisch für die Höhenabschnitte AH = 1, BH = 2, CH = 3.

restart: with(plots): with(plottools):

# Eingabe Höhenabschnitte:

AH := 1;

BH := 2;

CH := 3;

A := [xA, yA]:

B := [xB, yB]:

C := [xC, yC]:

H := [xH, yH]:

xC := 0: yC := CH:

xH := ((-yB + yC)*yA^2 + (yB^2 - yC^2 - (xB - xC)*xA)*yA - yB^2*yC + (yC^2 + (xA - xC)*xB)*yB - xC*yC*(xA - xB))/((-xB + xC)*yA + (xA - xC)*yB - yC*(xA - xB)):

yH := ((xB - xC)*xA^2 + (-xB^2 + xC^2 + yA*(yB - yC))*xA + xB^2*xC + (-xC^2 - yB*(yA - yC))*xB + xC*yC*(yA - yB))/((yB - yC)*xA + (-yA + yC)*xB + xC*(yA - yB)):

Distanz := proc(A, B) local Distanz :

Distanz := sqrt((B[1]-A[1])^2 + (B[2]-A[2])^2):

end proc:

GlgSys := {Distanz(A,H) = AH, Distanz(B,H) = BH, xH = 0, yH = 0.0}:

Loes := solve(GlgSys, [xA, yA, xB, yB]):

Die Schreibweise der Gleichung yH = 0.0 (mit Dezimalpunkt) hat zur Folge, dass in floating point arithmetic gerechnet wird. Das ist einfacher für die Kontrolle.

4 Mehrere Lösungen

Das Problem hat bis zu sechs Lösungen. Im Beispiel mit den Höhenabschnitten 1, 2, 3 sind vier Lösungen reell, zwei komplex.

Um die erste Lösung sichtbar zu machen, fahren wir fort:

assign(Loes[1]): # Nummer der Lösung

Punkt := proc(A, Farbe, Name) local Punkt :

Punkt := point(A, symbol = solidcircle, symbolsize = 20, color = Farbe):

end proc:

Linie := proc(A,B, Farbe) local Linie :

Linie := line(A, B, thickness = 3, color = Farbe):

end proc:

TextA := textplot([xA,yA,"A"], color = red, font=[Times, 24, italic],'align' = {'above', 'right'}):

TextB := textplot([xB,yB,"B"], color = red, font=[Times, 24, italic],'align' = {'above', 'right'}):

TextC := textplot([xC,yC,"C"], color = red, font=[Times, 24, italic],'align' = {'above', 'right'}):

TextH := textplot([xH,yH,"H"], color = blue, font=[Times, 24, italic],'align' = {'above', 'right'}):

display( [Punkt(H, blue), Linie(A,B, red),Linie(B,C, red),Linie(C,A, red),Linie(A,H, blue), Linie(B,H, blue), Linie(C,H, blue),Punkt(A, red), Punkt(B,red), Punkt(C,red), TextA, TextB, TextC, TextH],

scaling=constrained,

axis[1]=[thickness = 1, color=black, tickmarks=[spacing(1, 0), subticks=1] ],

axis[2]=[thickness = 1, color=black, tickmarks=[spacing(1, 0), subticks=1] ],

labels=[x,y],

axesfont=[Times, roman, 20],

labelfont=[TIMES, roman, 20]);

5 Die Lösungen

Die Abbildungen 1 bis 4 zeigen die reellen Lösungen. Je zwei Lösungen sind spiegelbildlich. Damit haben wir zwei wesentlich verschiedene reelle Lösungen.

Die Lösungen mit den Nummern 1 und 2 sind reell und spiegelbildlich.

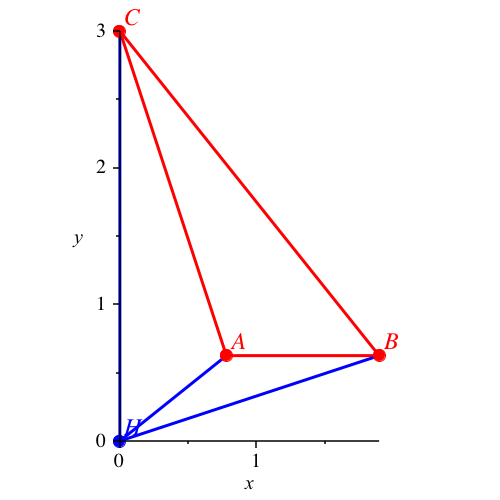
Abb. 1: Lösung Nummer 1

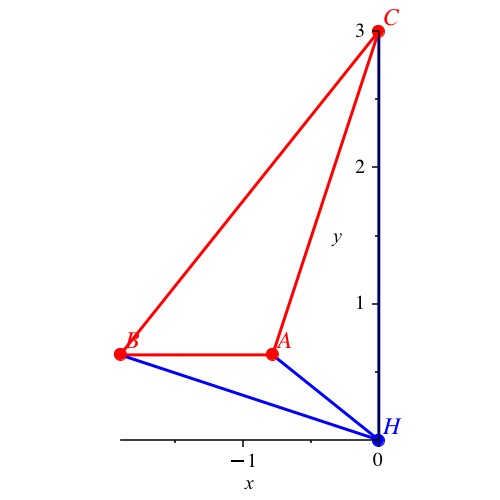
Abb. 2: Lösung Nummer 2

Die Lösungen mit den Nummern 3 und 4 haben teilweise imaginäre Koordinaten.

Die Lösungen mit den Nummern 5 und 6 sind reell und spiegelbildlich.

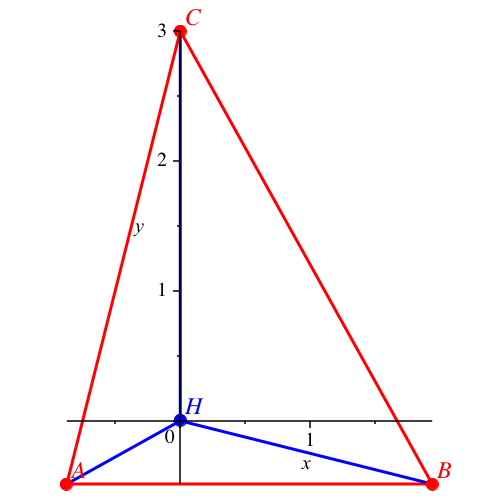
Abb. 3: Lösung Nummer 5

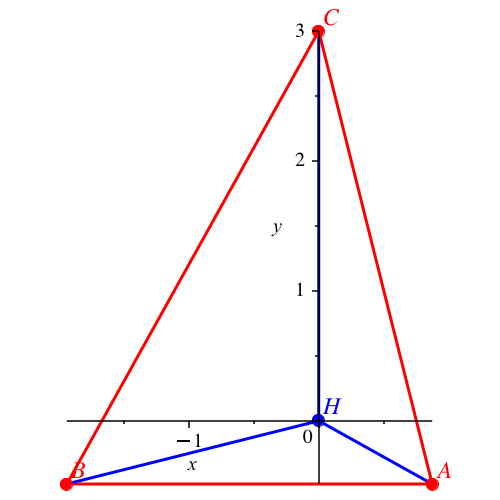
Abb. 4: Lösung Nummer 6

6 Redundanz

Da in unserer Disposition die Höhe h_c auf der y-Achse liegt, hätten wir eine fünfte Gleichung für unser Gleichungssystem, nämlich yA = yB. Diese Gleichung ist aber verträglich mit den vier anderen, also redundant. Dies ist wohl die algebraische Formulierung des Satzes vom Höhenschnittpunkt.

7 Konstruktive Lösung?

Eine konstruktive Lösung mit Zirkel und Lineal habe ich noch nicht probiert. Vielleicht bringt da der Satz von Segner etwas.

Weblink

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte/Hoehenabschnitte.htm