Hans Walser, [20230522]

Höhenabschnitte

Anregung: Hans Humenberger, Wien

1 Worum geht es?

Ein Problem der ebenen Geometrie wird mit einem räumlichen Pyramidenmodell gelöst.

2 Problem

Von einem spitzwinkligen Dreieck kennen wir die drei Abschnitte vom Höhenschnittpunkt zu den Ecken (Höhenabschnitte). Gesucht ist eine Rekonstruktion des Dreiecks.

3 Einsicht auf Vorrat

Die Abbildung 1 zeigt ein Dreieck mit den drei farbig markierten Höhenabschnitten.

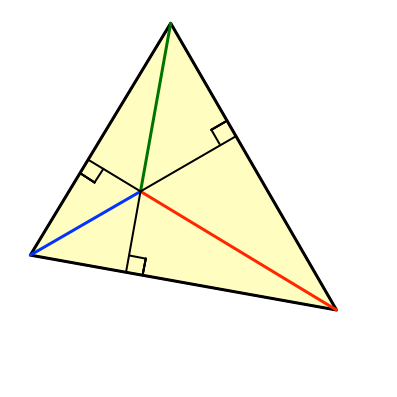
Abb. 1: Höhenabschnitte im Dreieck

Im hellblauen Viereck (Abb. 2) haben wir zwei gegenüberliegende rechte Winkel. Daher ergänzen sich die beiden anderen Winkel auf 180°.

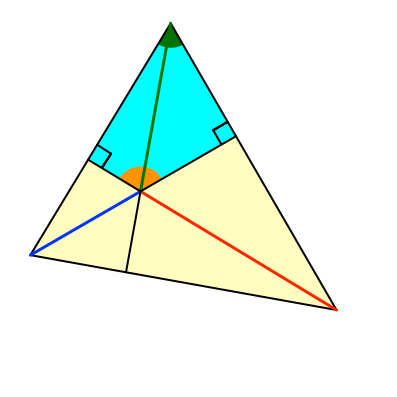
Abb. 2: Ergänzungswinkel

Diesen Ergänzungswinkel können wir weiterverfolgen (Abb. 3 und 4).

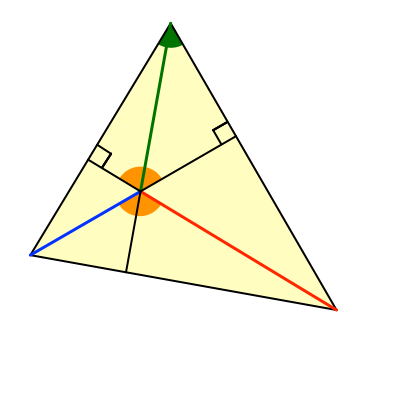
Abb. 3: Punktgespiegelter Ergänzungswinkel

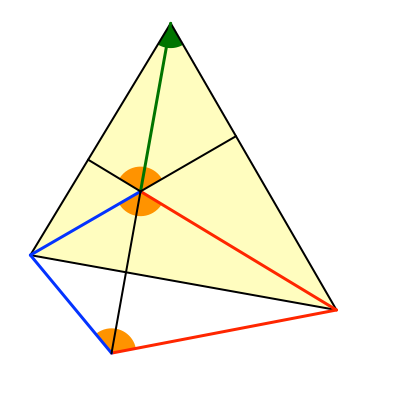
Abb. 4: Herausgeklappter Ergänzungswinkel

Nun haben wir aber ein Sehnenviereck (Abb. 5). Der herausgespiegelte Höhenschnittpunkt liegt auf dem Umkreis des Dreiecks.

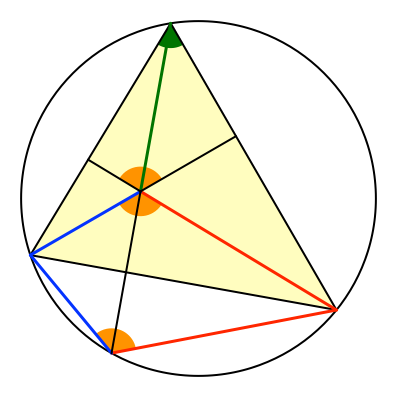
Abb. 5: Sehnenviereck

Analog können wir an den beiden anderen Seiten herausspiegeln (Abb. 6).

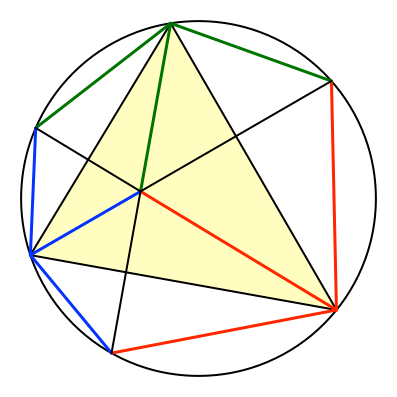
Abb. 6: Vollständiges Herausspiegeln

Wir erhalten ein Sehnensechseck. Sein Umkreis ist der Umkreis des Dreieckes, seine Seiten sind paarweise die Höhenabschnitte, in unserer Färbung also rot-rot-grün-grün-blau-blau (Abb. 7).

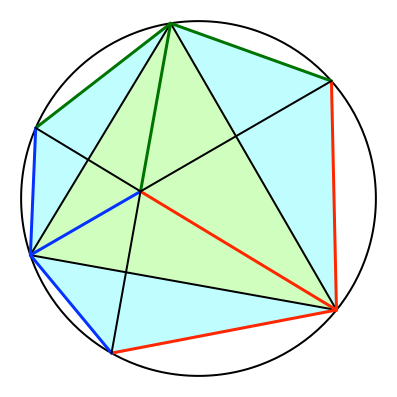
Abb. 7: Sehnensechseck

Von diesem Sehnensechseck kennen wir die Seiten, leider nicht den Umkreisradius. Um diesen zu finden, bauen wir eine Pyramide.

4 Schnittmuster der Pyramide

Wir beginnen mit einem beliebigen Kreis (Sie haben richtig gelesen: beliebiger Kreis. Allerding sollte er nicht zu klein sein). In diesen Kreis zeichnen wir den ersten Höhenabschnitt (die drei Höhenabschnitte sind ja bekannt) als Sehne ein und ergänzen zu einem gleichschenkligen Dreieck zur Kreismitte (Abb. 8).

Abb. 8: Kreis mit Sehne und Dreieck

An dieses Dreieck schließen wir ein gleiches Dreieck an, dann zwei weitere Dreiecke mit dem zweiten Höhenabschnitt als Sehne, dann zwei Dreiecke mit dem dritten Höhenabschnitt als Sehne und schließlich noch einmal das erste Dreieck (Abb. 9).

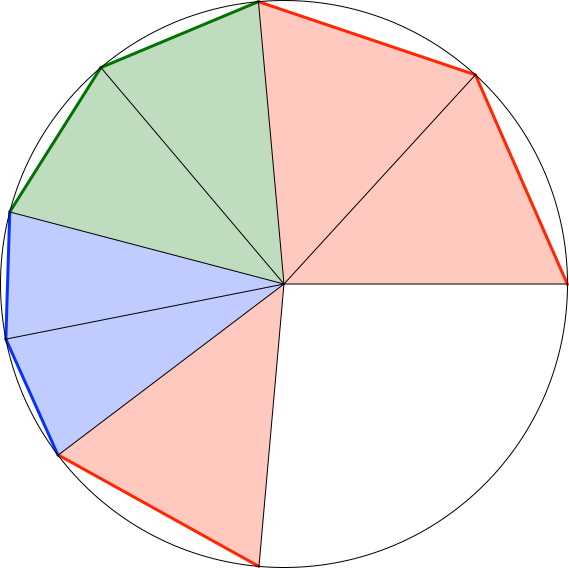
Abb. 9: Weitere Dreiecke

Es bleibt eine Lücke übrig. Falls sich die Dreiecke aber überlappen, haben wir Pech gehabt und müssen mit einem größeren Kreis nochmals beginnen.

5 Bau der Pyramide

Wir schneiden die Figur mit den Dreiecken aus (Abb. 10) und falten längs der radialen Linien.

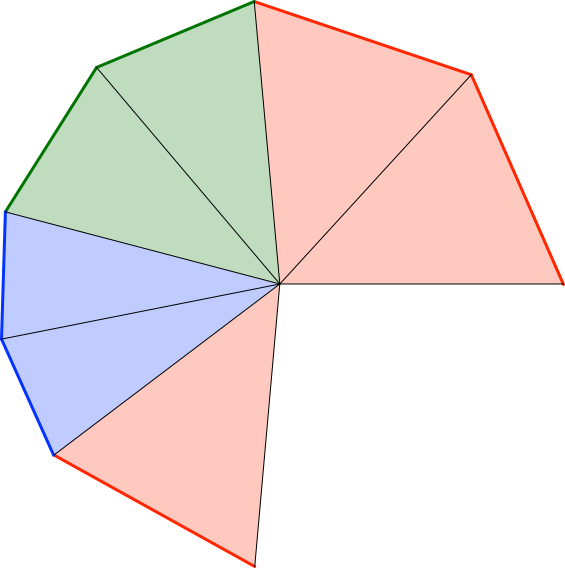
Abb. 10: Ausschneiden und Falten

Nun können wir die Pyramide bauen. Wir verheften das letzte rote Dreieck mit dem ersten, indem wir die beiden Dreiecke übereinanderlegen und fixieren, zum Beispiel mit Büroklammern oder Leim oder Tackern (Abb. 11). Wir stellen die Pyramide auf ein Zeichenpapier. Allenfalls müssen wir mit dem Finger an der Spitze sanften Druck ausüben, damit alle Bodenkanten der Pyramide flach aufliegen.

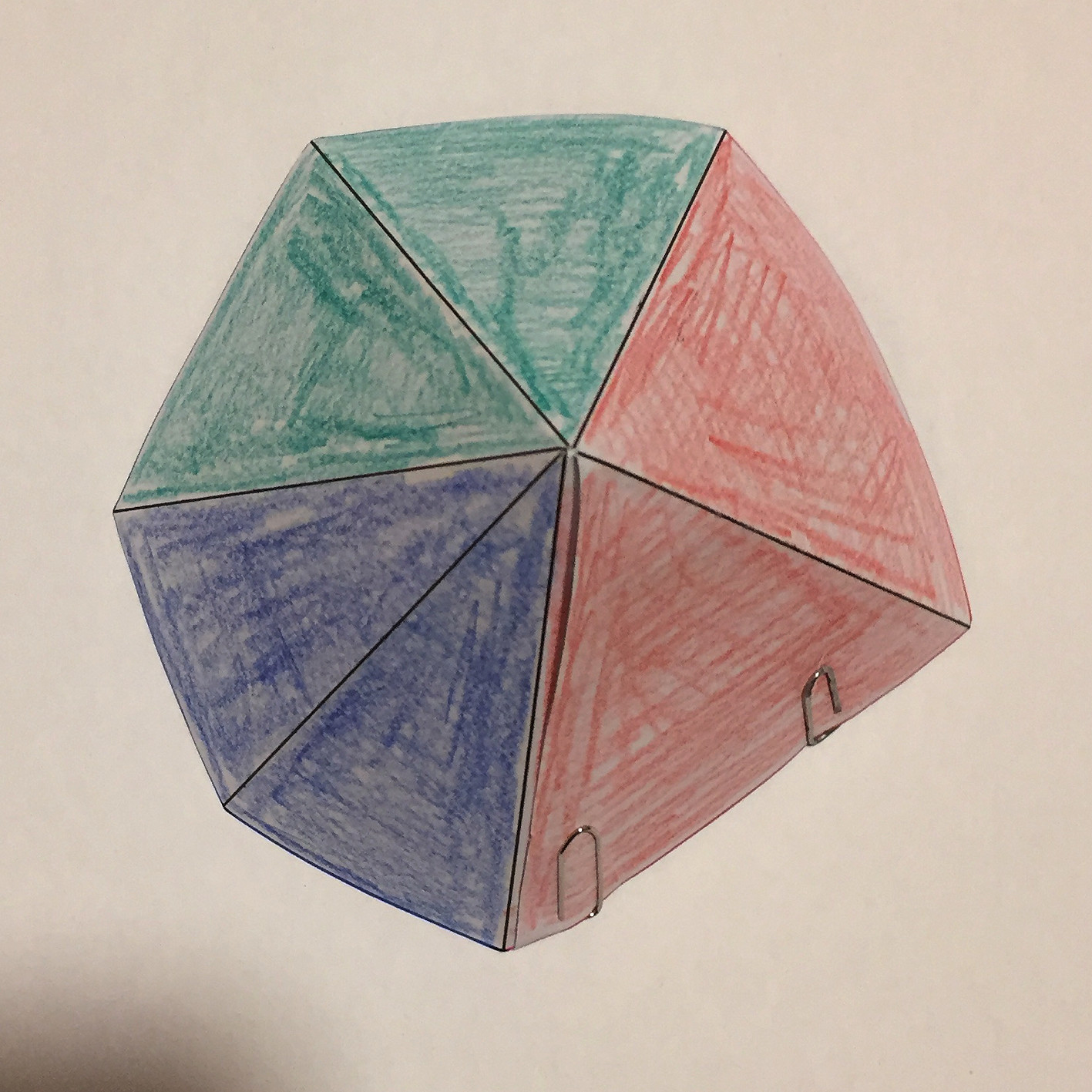
Abb. 11: Die Pyramide

In der Sicht genau von oben sehen wir als Bodenumriss das Sechseck der Abbildung 7.

Wir übertragen nun diejenigen Sechseckecken, an denen zwei gleichfarbige Dreiecke liegen, auf die Papierunterlage.

Die drei markierten Punkte sind die Ecken des gesuchten Dreieckes.

Man kann nun mit dem guten alten Geodreieck das Dreieck ergänzen, die Höhen einzeichnen und die Höhenabschnitte nachkontrollieren. Stimmt.

Weblinks

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte2/Hoehenabschnitte2.html

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte/Hoehenabschnitte.htm