Hans Walser, [20130222a]
Hhensatz
Anregung: L. H.-H.
1 Arbelos und Kreis des Archimedes
Die Abbildung 1 zeigt rot das ãSchustermesserÒ (Arbelos) und blau den Kreis des Archimedes.
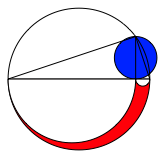
Abb. 1: Rot = Blau
Die beiden Figuren sind flchengleich. Zum Beweis kann der Hhensatz verwendet werden.
Der Kreis des Archimedes hat die Dreieckshhe als Symmetrieachse. Der Arbelos bercksichtigt die beiden Hypotenusenabschnitte in gleicher Weise.
2 Der unschne Hhensatz
Natrlich ist der Hhensatz selber schn, nur die in der Schule blichen Visualisierungen sind es nicht. Die Abbildung 2 zeigt vier Visualisierungen des Hhensatzes. Keine dieser Darstellungen ist bezglich der Dreieckshhe ausgeglichen. Das Hhenquadrat liegt asymmetrisch zur Dreieckshhe, von den beiden Hypotenusenabschnitten ist einer waagerecht, der andere senkrecht verarbeitet.
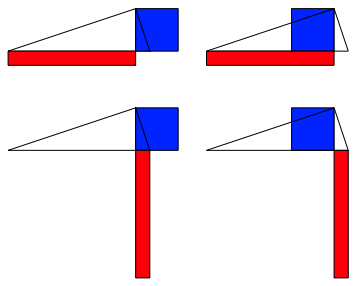
Abb. 2: Rot = Blau
3 Der schne Hhensatz
Die Frage ist, ob die Figur der Abbildung 1 ãvereckigtÒ werden kann, so dass eine ausgeglichene Visualisierung des Hhensatzes entsteht.
Die Abbildung 3 zeigt einen Lsungsvorschlag. Bis auf den Thaleskreis sind alle Kreise vereckigt worden.
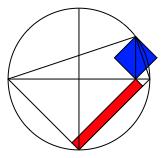
Abb. 3: Rot = Blau
Die Flchenstcke sind im Vergleich zu denen der Abbildung 2 halb so gro§.
4 Variationen
Die Abbildung 4 zeigt drei Variationen.
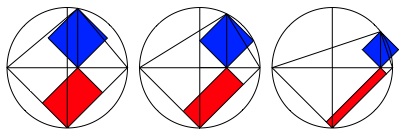
Abb. 4: Drei Variationen
In allen drei Beispielen ist die obere Quadratecke auf dem Thaleskreis, die untere Quadratecke im Hhenfu§punkt des rechtwinkligen Dreieckes.
Interessant sind die linke und die rechte Quadratecke. In der ersten Figur liegen die linke Quadratecke links von der senkrechten Linie des Fadenkreuzes und die rechte Quadratecke innerhalb des Thaleskreises. In der mittleren Figur liegen die linke Quadratecke genau auf der senkrechten Linie des Fadenkreuzes und zudem die rechte Quadratecke genau auf dem Thaleskreis. In der dritten Figur liegen die linke Quadratecke rechts der senkrechten Linie des Fadenkreuzes und die rechte Quadratecke au§erhalb des Thaleskreises. Die Abbildung 5 zeigt die Bahnkurve der linken Quadratecke (magenta) und der rechten Quadratecke (zyan).
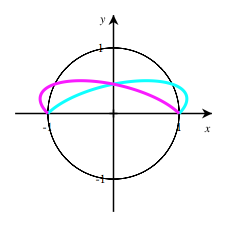
Abb. 5: Bahnkurven
Diese Bahnkurven haben die Parameterdarstellungen:
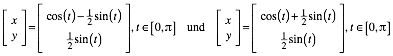
Es handelt sich um halbe Ellipsen.
5 Sonderfall und Goldener Schnitt
Interessant ist der bergangsfall der mittleren Figur in Abbildung 4. In diesem Fall sind die Kathetenlngen des rechtwinkligen Dreiecks im Verhltnis des Goldenen Schnitts. Das Dreieck kann zu einem Goldenen Rechteck ergnzt werden (Abb. 6).
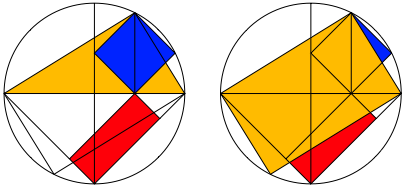
Abb. 6: Goldenes Rechteck
Das Verhltnis des Goldenen Schnittes findet sich auch anderswo. Die Abbildung 7 zeigt zwei Beispiele. Der Major ist jeweils blau, der Minor rot eingetragen.
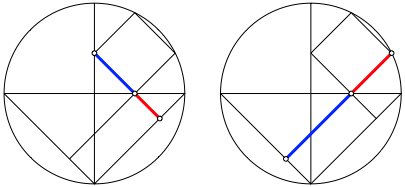
Abb. 7: Verhltnis des Goldenen Schnittes