Hans Walser, [20120318a]
Hhensatz
Der Hhensatz wird blicherweise ber die hnlichkeit der beiden durch die Hhe gebildeten Teildreiecke (Abb. 1) bewiesen.
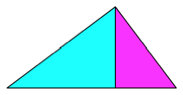
Abb. 1: Teildreiecke
Es geht aber auch mit
einer Flchenberlegung:
Wir drehen eines der
beiden Teildreiecke um einen rechten Winkel und betten die Gesamtfigur in ein
Rechteck ein (Abb. 2).
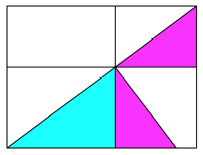
Abb. 2: Einbettung in
Rechteck
Dann lsst sich die
Flchengleichheit des Hhenquadrates mit dem Rechteck aus den
Hypotenusenabschnitten unmittelbar ablesen (Abb. 3).
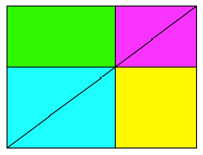
Abb. 3: Gelb = grn
Diese Flchenberlegung
geht auf die chinesische Mathematik zurck [Swetz 2012].
Literatur
[Swetz
2012] Swetz,
Frank J.: Similarity vs. The ãIn-and-Out Complementary PrincipleÒ: A Cultural
Faux Pas. Mathematics Magazine. 85 (2012), p. 3-11.