Hans Walser, [20210726]

Höhensatz –> Pythagoras

Anregung: Gerwig (2021)

0 Worum geht es?

Beweis des Satzes des Pythagoras aus dem Höhensatz

1 Höhensatz

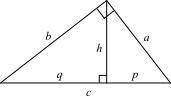
Abb. 1: Bezeichnungen

Mit den Bezeichnungen der Abbildung 1 lautet der Höhensatz:

(1)

1.1 Beweis mit Ähnlichkeit

Aus der Ähnlichkeit der beiden Teildreiecke folgt:

(2)

1.2 Beweis mit dem Satz des Pythagoras

Einerseits:

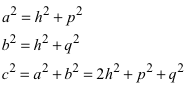(3)

Andererseits (binomische Formel):

(4)

Vergleich von (3) und (4) ergibt (1).

1.3 Zerlegungsbeweis

Der Zerlegungsbeweis (Abb. 2) läuft wie auf Schienen.

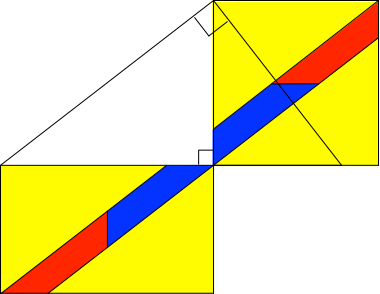
Abb. 2: Zerlegungsbeweis für den Höhensatz

2 Ähnliche Dreiecke

Ähnliche Figuren haben nicht nur gleiche Längenverhältnisse, sondern auch gleich Flächen- und Volumenverhältnisse.

Zwei Dreiecke sind ähnlich, wenn sie in zwei Winkeln, zum Beispiel a und b übereinstimmen. Somit ist in der üblichen Notation für zwei ähnlich Dreiecke:

(5)

Bei ähnlichen rechtwinkligen Dreiecken haben wir nur noch einen freien Parameter, zum Beispiel a. Somit gilt bei ähnlichen rechtwinkligen Dreiecken:

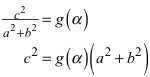(6)

Hier muss beachtet werden, dass wir den Satz des Pythagoras noch nicht kennen. Wir können also nicht sagen, dass g die Konstante 1 ist.

3 Pythagoras

Wir leiten den Satz des Pythagoras aus dem Höhensatz ab. Da dieser mit Ähnlichkeit (also ohne Pythagoras) hergeleitet werden kann (Abschnitt 1.1), haben wir keinen Zirkelschluss.

Formelturnen. Aus (1) folgt:

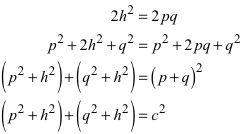(7)

Die Abbildung 3 illustriert den Sachverhalt (7).

Abb. 3: Rot = blau

Die Abbildung 4 gibt einen Zerlegungsbeweis dazu.

Abb. 4: Gemeinsame Zerlegung

Die drei in der Figur sichtbaren rechtwinkligen Dreiecke sind ähnlich. Wir können die Formel (6) dreimal anwenden. Es ist:

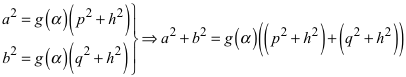(8)

Weiter ist, ebenfalls nach (6):

(9)

Ais (7), (8) und (9) ergibt sich:

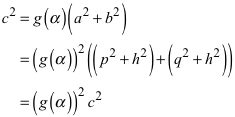(10)

Somit ist:

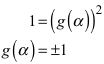(11)

Da g in unserem Kontext positiv ist, haben wir für g die Konstante 1. Aus (9) folgt damit der Satz des Pythagoras.

Die rechnerische Grundidee dieses Beweises ist die Bestimmung der mittleren Proportionalen.

4 Äquivalenz

Der Höhensatz und der Satz des Pythagoras sind äquivalent.

5 Beliebiges Dreieck

Für die Funktion f in (5) gilt:

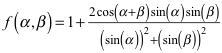(12)

Dies kann mit dem Kosinussatz und dem Sinussatz hergeleitet werden. Die Abbildung 5 zeigt den Funktionsgrafen und die Niveaulinien. Wir sehen das konstante Niveau 1 (hellblau) für:

(13)

Dies sind die rechtwinkligen Dreiecke. Dies ist aber kein Beweis für den Satz des Pythagoras, da bei der Herleitung von (12) der Kosinussatz und damit der Satz des Pythagoras benutzt wurde.

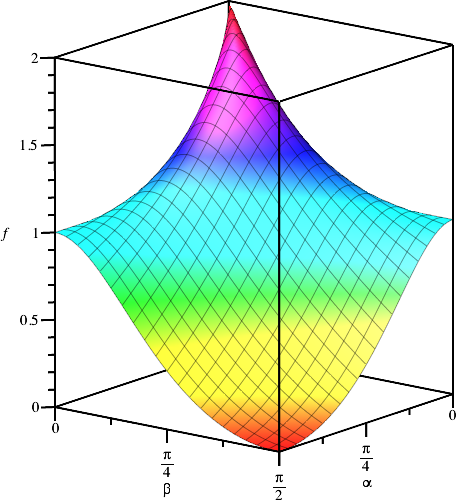
Abb. 5a: Funktionsgraf

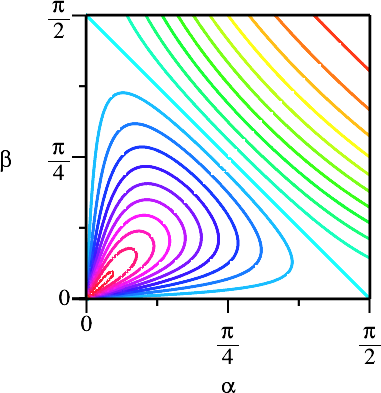
Abb. 5b: Niveaulinien

Literatur

Gerwig, Mario (2021): Der Satz des Pythagoras in 365 Beweisen. Mathematische, kulturgeschichtliche und didaktische Überlegungen zum vielleicht berühmtesten Theorem der Mathematik. Mit einem Geleitwort von Günter M. Ziegler. Springer Spektrum. ISBN 978-3-662-62885-0. ISBN 978-3-662-62886-7 (eBook). https://doi.org/10.1007/978-3-662-62886-7

Websites

Hans Walser: Höhensatz

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehensatz2/Hoehensatz2.htm

Hans Walser: Höhensatz

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehensatz1/Hoehensatz1.htm

Hans Walser: Visualisierungen des Höhensatzes

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehensatz/Hoehensatz.htm