1 Worum es geht

Kollineare Punkte und Höhenschnittpunkt im Dreieck.

Numerisch verifiziert. Formaler Beweis fehlt.

2 Vorgehen

In einem Dreieck (grau in Abb. 1) zeichnen wir die drei Ellipsen, welche je zwei Dreieckspunkte als Brennpunkte haben und durch den dritten Dreieckspunkt verlaufen. Zu diesen Ellipsen zeichnen wir je die „spitzen Scheitelpunkte“.

Abb. 1: Drei Ellipsen

Jeder Dreieckspunkt ist also gemeinsamer Brennpunkt von genau zwei der drei Ellipsen.

Nun zeichnen wir zu jedem Dreieckspunkt die Gerade durch die Perihelpunkte (nächstliegende spitze Scheitel) dieser beiden Ellipsen (orange in Abb. 2). Diese drei Geraden definieren ein Dreieck.

Abb. 2: Geraden durch Perihelpunkte

Analog zeichnen wir die Geraden durch die Aphelpunkte (entfernt liegende spitze Scheitel) (lila in Abb. 3).

Abb. 3: Geraden durch Aphelpunkte

Wir haben jetzt drei Dreiecke, das graue Startdreieck, das orange Periheldreieck und das lila Apheldreieck.

3 Kollineare Punkte

Es gilt:

1. Je drei Eckpunkte der drei Dreiecke liegen auf einer Geraden (dick rot in Abb. 4).

2. Die drei roten Geraden schneiden sich in einem Punkt.

3. Die drei roten Geraden sind senkrecht zu den Seiten des grauen Dreiecks, also seine Höhen. Der gemeinsame Punkt ist der Höhenschnittpunkt.

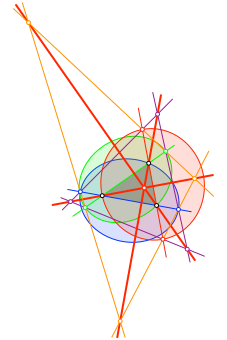
Abb. 4: Kollineare Punkte. Höhenschnittpunkt

Ich habe keinen formalen Beweis gefunden.

Weblinks

Hans Walser: Lotvermutung

https://walser-h-m.ch/hans/Miniaturen/L/Lotvermutung/Lotvermutung.html

Hans Walser: Höhenschnittpunkt ohne Höhen

https://walser-h-m.ch/hans/Miniaturen/H/Hoehenschnittpunkt/Hoehenschnittpunkt.htm