1 Wörter

1.1 Ein Beispiel

Wir nehmen einen beliebigen Text mit einigen Zeilen.

Am Anfang schuf Gott Himmel und Erde. Und die Erde war wüst und leer, und es war finster auf der Tiefe; und der Geist Gottes schwebte auf dem Wasser.

Text

Nun markieren wir das erste Wort, zum Beispiel mit blauer Farbe. Wir zählen die Anzahl der Buchstaben dieses Wortes (in unserem Beispiel 2) und hüpfen die gleiche Anzahl Wörter weiter, wo wir wieder markieren. Nun zählen wir wieder die Buchstaben und hüpfen die gleiche Anzahl Wörter weiter. Und so weiter und so fort. Wo landen wir?

Am Anfang schuf Gott Himmel und Erde. Und die Erde war wüst und leer, und es war finster auf der Tiefe; und der Geist Gottes schwebte auf dem Wasser.

Blauer Weg

Was geschieht, wenn wir erst beim zweiten Wort starten?

Am Anfang schuf Gott Himmel und Erde. Und die Erde war wüst und leer, und es war finster auf der Tiefe; und der Geist Gottes schwebte auf dem Wasser.

Roter Weg

Wir sehen, dass wir in unserem Beispiel wieder beim Wort Gottes enden.

Beim dritten Wort starten hat wenig Sinn, weil wir da gleich in den blauen Weg einsteigen.

Wenn wir beim vierten Wort starten, enden wir wieder beim Wort Gottes (grüner Weg)

Am Anfang schuf Gott Himmel und Erde. Und die Erde war wüst und leer, und es war finster auf der Tiefe; und der Geist Gottes schwebte auf dem Wasser.

Grüner Weg

Auch wenn wir beim fünften Wort starten, enden wir beim Wort Gottes (rosa Weg).

Am Anfang schuf Gott Himmel und Erde. Und die Erde war wüst und leer, und es war finster auf der Tiefe; und der Geist Gottes schwebte auf dem Wasser.

Rosa Weg

Enden wir immer beim Wort Gottes?

Das erste Startwort, bei welchem wir bei einem anderen Wort enden, ist das Wort war in der zweiten Zeile (oranger Weg).

Am Anfang schuf Gott Himmel und Erde. Und die Erde war wüst und leer, und es war finster auf der Tiefe; und der Geist Gottes schwebte auf dem Wasser.

Oranger Weg

Gibt es weitere Startwörter, deren Weg nicht beim Wort Gottes endet?

Wie ist es bei einem längeren Text?

Im folgenden Beispiel gibt es drei durchgehend verschiedene Wege.

Bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla.

Es gibt drei verschiedene Wege

1.2 Wahrscheinlichkeitsabschätzung

Wir starten in einem beliebigen Text mit dem ersten Wort und erhalten so einen Weg, den wir als blauen Weg bezeichnen. Nun schätzen wir die Wahrscheinlichkeit ab, bei einem anderen Startwort (roter Weg) nicht auf den blauen Weg aufzufahren. Es zeigt sich, dass diese Wahrscheinlichkeit klein ist.

Es sei n die Anzahl der im Text vorkommenden Wörter, m die maximal vorkommende Wortlänge.

Einen zweiten (roten) Weg starten wir beim Wort Nr. k. Der rote Weg hat also Schritte.

Für die Abschätzung der Wahrscheinlichkeit treffen wir die Annahme, die Wortlängen im Text seien gleichverteilt. Diese Annahme ist bei einem realen Text nicht erfüllt, die kurzen Wörter sind häufiger als Wörter in der Nähe der maximalen Wortlänge. Dieser reale Sachverhalt verschärft aber die nachfolgende Abschätzung.

Die Wahrscheinlichkeit, dass wir im roten Weg nach einem Schritt nicht auf den blauen Weg auffahren, ist .

Die Wahrscheinlichkeit, dass wir auf dem ganzen roten Weg nicht auf den blauen Weg auffahren, ist . Wenn wir k festhalten und , ergibt sich für diese Wahrscheinlichkeit der Grenzwert null.

2 Münzenreihe

Wir werfen (gleiche) Münzen und bringen sie auf eine Reihe. Wir wählen eine Startmünze. Falls sie Kopf zeigt, gehen wir eine Münze weiter, andernfalls zwei Münzen.

Die Abbildung zeigt ein Beispiel mit zwei verschiedenen Startmünzen (blauer Weg und roter Weg).

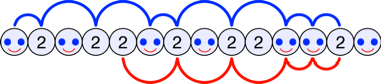
Blauer Weg und roter Weg

Ist es überhaupt möglich, dass es zwei Wege gibt, die nicht bei derselben Münze enden?

Mit einiger Überlegung finden wir, dass das nur möglich ist, wenn wir ausschließlich Münzen mit Zahl haben. Sobald ein Kopf erscheint, gibt es ab der folgenden Münze nur noch einen Weg.

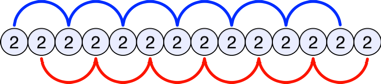
Zwei verschiedene Wege

Bei n Münzen ist die Wahrscheinlichkeit dazu , also sehr klein.

3 Würfelreihe

Das Beispiel findet sich im Mathematikum in Gießen.

Wir würfeln und setzen die geworfenen Würfel zu einer Reihe zusammen. Dann wählen wir einen Startwürfel und rücken dessen Augenzahl weiter.

Wir enden fast immer beim gleichen Würfel.

Es ist aber durchaus möglich, dass es zwei Wege mit verschiedenem Endwürfel gibt. Dies ist zum Beispiel dann der Fall, wenn alle Würfel dieselbe Augenzahl (größer als 1) zeigen.