1 Worum geht es?

HP-Flächen auf dualen Tetraedern

2 Hyperbolischer Rhombus im Raum

Die Abbildung 1a zeigt ein gleichseitiges, aber nicht ebenes Viereck im Raum.

Abb. 1: Rhombus im Raum. HP-Fläche

Zwischen zwei gegenüberliegende Seiten spannen wir in gleichmäßigen Abständen Strecken als Lattung ein (Abb. 1b). Diese Strecken generieren eine HP-Fläche.

Aus Symmetriegründen enthält die Fläche eine zweite Streckenschar, die Konter-Lattung (Abb. 2a).

Abb. 2: Konter-Lattung. Hyperbolischer Rhombus

In den folgenden Abbildungen werden wir die Lattung und die Konter-Lattung weglassen und nur den hyperbolischen Rhombus (Abb. 2b) zeichnen.

3 Duale Tetraeder im Würfel

Einem Würfel schreiben wir durch alternierende Auswahl der Würfelecken zwei duale Tetraeder ein.

In die vier Ecken einer Würfelseite spannen wir eine HP-Fläche ein. Die HP-Flächen sind vorderhand eben, nämlich die Seitenquadrate des Würfels (Abb. 3a). — Die nicht sichtbare Würfelseite gegenüber der roten ist cyan, gegenüber der grünen magenta und gegenüber der blauen gelb (komplementäre rgb-Farben).

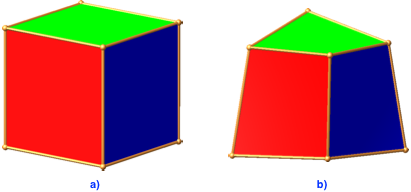
Abb. 3: Würfel. Deformation mit t = 0.8

4 Variation eines Tetraeders

Nun strecken wir das eine der beiden Tetraeder vom Mittelpunkt aus mit dem Faktor t. Dadurch werden die Kanten der Seitenflächen des Würfels windschief und wir erhalten „echte“ HP-Flächen, in unserem Fall also hyperbolische Rhomben (Abb. 3b für t = 0.8).

5 Beispiele

Im Folgenden Beispiele für verschiedene Werte von t.

Bei t = 0.5 wird allmählich die Form eines Tetraeders sichtbar (Abb. 4a).

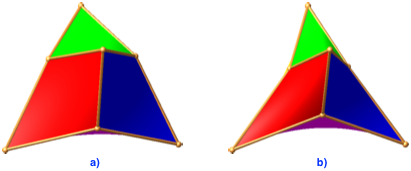
Abb. 4: t = 0.5 und t = ein Drittel

Bei t = ein Drittel sind die Ecken des verkleinerten Tetraeders die Seitenflächenmittelpunkte des anderen Tetraeders (Abb. 4b). Diese Figur wird in Giering (2021, Abb. 1) beschrieben.

Für t = 0 haben wir eine volumenlose Figur (Abb. 5a). Wir erhalten sechs Schwimmhäute, welche eingespannt sind in die vom Mittelpunkt zu den Tetraederecken verlaufenden Strecken. Die Außenkontur der Schwimmhäute ist jeweils eine Bézier-Kurve zweiten Grades, also eine Parabel. In der Abbildung 5b sind zur Verdeutlichung lediglich die beiden ursprünglich gegenüberliegenden Flächen grün und magenta gezeichnet.

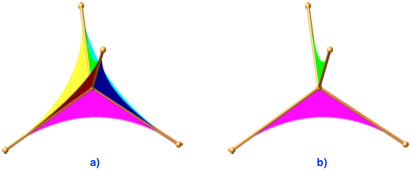
Abb. 5: Volumenlose Figur für t = 0

Bei t = – 0.5 erhalten wir eine Figur mit Selbstdurchdringungen (Abb. 6).

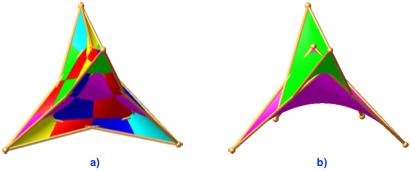
Abb. 6: t = – 0.5

Bei t = – 0.99 fallen die beiden Tetraeder fast aufeinander (Abb. 7).

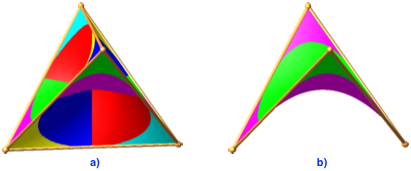
Abb. 7: t = – 0.99

Für t = – 1 fallen die beiden Tetraeder zusammen. Daher fallen auch gegenüberliegende Rhomben zusammen. In der Abbildung 8 sind daher nur die Farben rot, grün und blau gezeichnet. Die Durchdringungskurven der hyperbolischen Rhomben sind Geraden (Abb. 8b). Es sind dies die Verbindungsstrecken gegenüberliegender Kantenmitten des Tetraeders.

Abb. 8: t = – 1

In einem passenden kartesischen Koordinatensystem (Abb. 9a) kann ein hyperbolischer Rhombus durch die Paraboloid-Gleichung z = xy beschrieben werden.

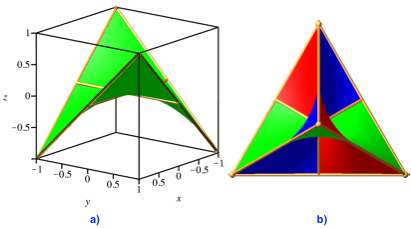
Abb. 9: Im Koordinatensystem. Sicht auf eine Ecke

Die Abbildung 9b zeigt die Sicht auf eine Tetraeder-Ecke.

6 Animation

Die Abbildung 10 gibt eine Animation bezüglich t.

Abb. 10: Variation von t

Literatur und Websites

Giering, Oswald (2020): Mit HP-Flächen variierte Platonische Polyeder I. IBDG. Informationsblätter der Geometrie. Heft 1/2021. Jahrgang 40. S. 37-38.

Giering, Oswald (2021): Mit HP-Flächen variierte Platonische Polyeder II. IBDG. Informationsblätter der Geometrie. Heft 2/2020. Jahrgang 39. S. 57-59.

Walser, Hans (2009): Fadengrafik.
www.walser-h-m.ch/hans/Miniaturen/F/Fadengrafik/Fadengrafik.htm