Hans Walser, [20200119]
Iglu und Kardioide
1 Worum geht es?
Das Ziel ist, eine halbkugelfrmige Kuppel mit mglichst wrfelfrmigen Bauelementen zu bauen.
Es erscheint eine Kurve, die mit der Kardioide verwandt ist.
2 Die Sicht von au§en
Die Abbildung 1 zeigt eine Halbkugel mit der blichen Parametrisierung mit einer 15¡-Rasterung der Meridiane und Breitenkreise.

Abb. 1: Halbkugel
Wir erkennen unten praktisch quadratische Elemente. Gegen den Pol zu werden die Elemente immer schmaler und immer deutlicher trapezfrmig.
Die Abbildung 2 zeigt die Halbkugel mit einer konformen Parametrisierung (ãAbbildung durch kleinste QuadrateÒ).

Abb. 2: Quadrate
An den Meridianen hat sich nichts gendert, die Rasterung ist nach wie vor 15¡. Die Breitenkreise hingegen werden gegen den Pol zu immer dichter. Die Elemente sind annhernd quadratisch.
Die Abbildung 3 zeigt die Quadrate schachbrettfrmig gefrbt.
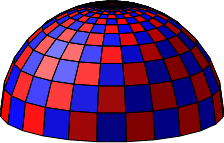
Abb. 3: Schachbrettfrbung
Die Abbildung 4 zeigt die aufgeschnittene Au§enschale.
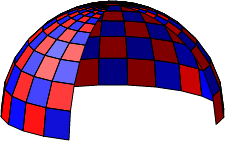
Abb. 4: Aufgeschnittene Au§enschale
3 Bauelemente
Die Seitenlnge der Quadrate ist proportional zum Kosinus der geografischen Breite.
Dies soll nun auch die dritte Dimension der Bauelemente sein. Die Kuppel wird also gegen den Pol zu immer dnner.
4 Bau
Die Abbildung 5 zeigt den Baubeginn. Wir erkennen die annhernd wrfelfrmigen Bauteile.
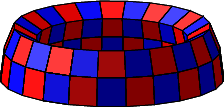
Abb. 5: Baubeginn
Die Animation 1 zeigt den zonalen Aufbau.

Animation 1: Zonaler Aufbau
Die Abbildungen 6 und 7 zeigen die aufgeschnittene Kuppel in zwei verschiedenen Beleuchtungen.
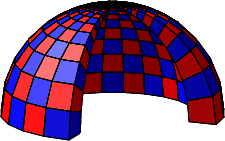
Abb. 6: Aufgeschnittene Kuppel
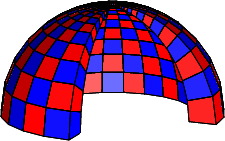
Abb. 7: Andere Beleuchtung
Die Animation 2 zeigt den sektoriellen Aufbau.

Animation 2: Sektorieller Aufbau
Die Animation 3 zeigt den elementweisen Aufbau.

Animation3: Elementweiser Aufbau
Die Innenschale der Kuppel ist keine Halbkugel (Abb. 8). Sie hat oben eine Spitze.

Abb. 8: Innenschale
5 Profil der Innenschale
Im Beispiel der Abbildung 8 liegt das Profil der Innenschale auf der Kurve (Abb. 9) mit der Polardarstellung:
![]() (1)
(1)
Kartesisch:
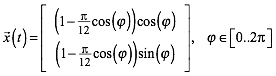 (2)
(2)
Der
Ausdruck ![]() ist die
Wrfelseite auf der geografischen Breite
ist die
Wrfelseite auf der geografischen Breite ![]() bei einer
15¡-Rasterung der Meridiane. Diese wird vom Kugelradius (welcher 1 gewhlt
wurde) subtrahiert.
bei einer
15¡-Rasterung der Meridiane. Diese wird vom Kugelradius (welcher 1 gewhlt
wurde) subtrahiert.

Abb. 9: Profilkurve
Die Kurve sieht aus wie ein Kreis, ist aber keiner.
6 Kurvenschar
Die Kurve gehrt zur Kurvenschar mit der Polargleichung:
![]() (3)
(3)
Die Abbildung 10 zeigt die Kurvenschar fr a von –1.5 bis +1.5 in Schritten von 0.1.
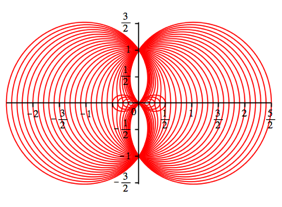
Abb. 10: Kurvenschar
Die Animation 4 zeigt dieselbe Kurvenschar.

Animation 4: Kurvenschar
Fr a = 0 erhalten wir den Einheitskreis, fr a = 1 die Kardioide (Abb. 11). Beweis rechnerisch.
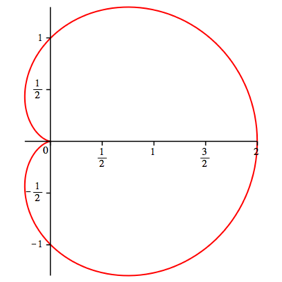
Abb. 11: Kardioide
Websites
Hans Walser: Kardioide als Spiegelbild der Parabel bei Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide2/Kardioide2.htm
Hans Walser: Kardioide und Goldener Schnitt
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide/Kardioide.htm
Hans Walser: Kardioide und regelm§ige Vielecke
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide3/index.html
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve/Herzkurve.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve2/Herzkurve2.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve3/Herzkurve3.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve4/Herzkurve4.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve5/Herzkurve5.htm
Hans Walser: Herzkurve und die Mndchen des Hippokrates
www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve_u_Hippokrates/Herzkurve_u_Hippokrates.htm
Hans Walser: Herzkurven
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurven/Herzkurven.htm