Hans Walser, [20220820]

Ikosaeder-Stern

1 Worum geht es?

Ikosaeder-Variante

2 Konstruktion

Wir gehen von einem regelmäßigen Dodekaeder aus (Abb. 1) und zeichnen die Seitenflächendiagonalen ein (Abb. 2).

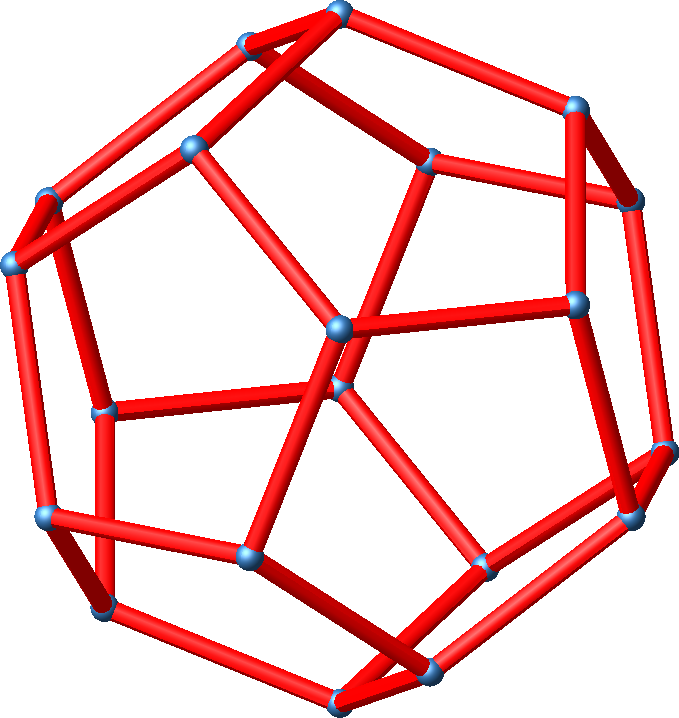
Abb. 1: Dodekaeder

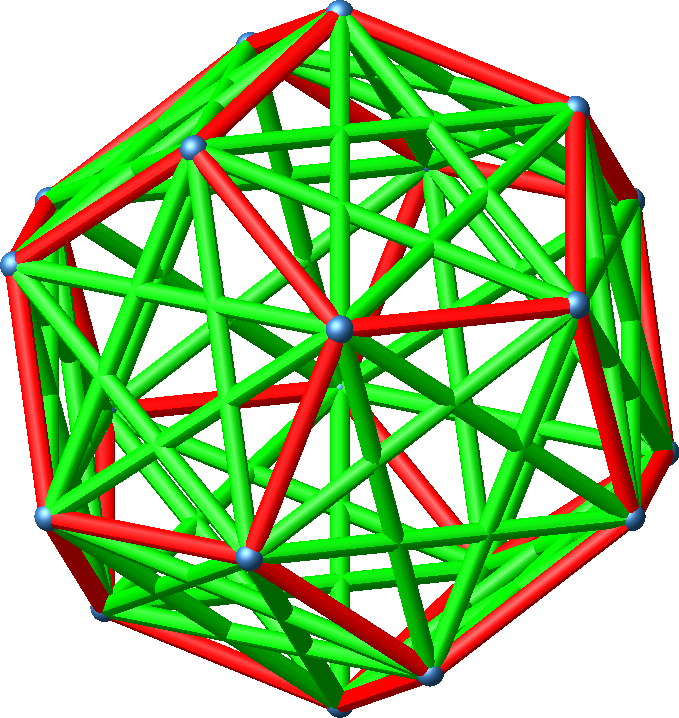
Abb. 2: Seitenflächendiagonalen

Nun sehen wir gleichseitige Dreiecke. In der Abbildung 3 ist ein solches gleichseitiges Dreieck eingezeichnet.

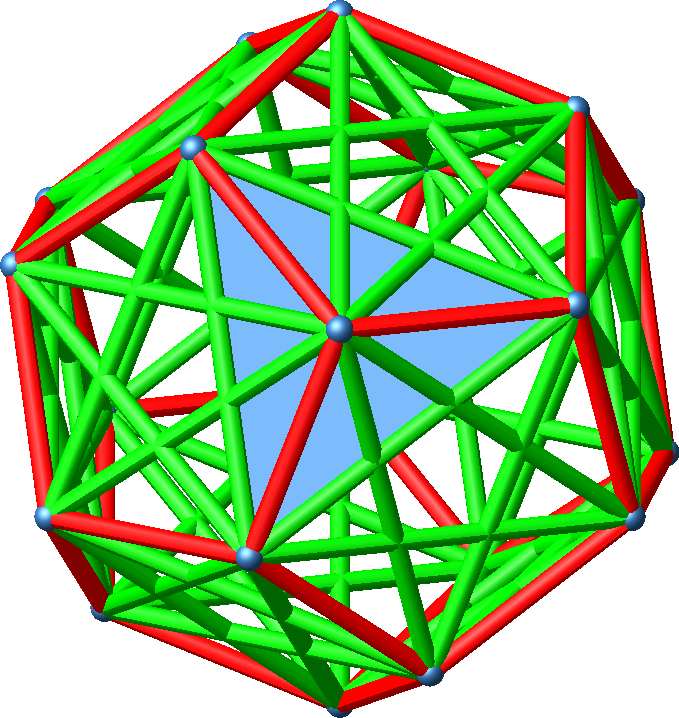
Abb. 3: Gleichseitiges Dreieck

Unter jeder Dodekaeder-Ecke liegt ein solches gleichseitiges Dreieck. Da das Dodekaeder 20 Ecken hat, gibt es entsprechend 20 solche gleichseitige Dreiecke (Abb. 4).

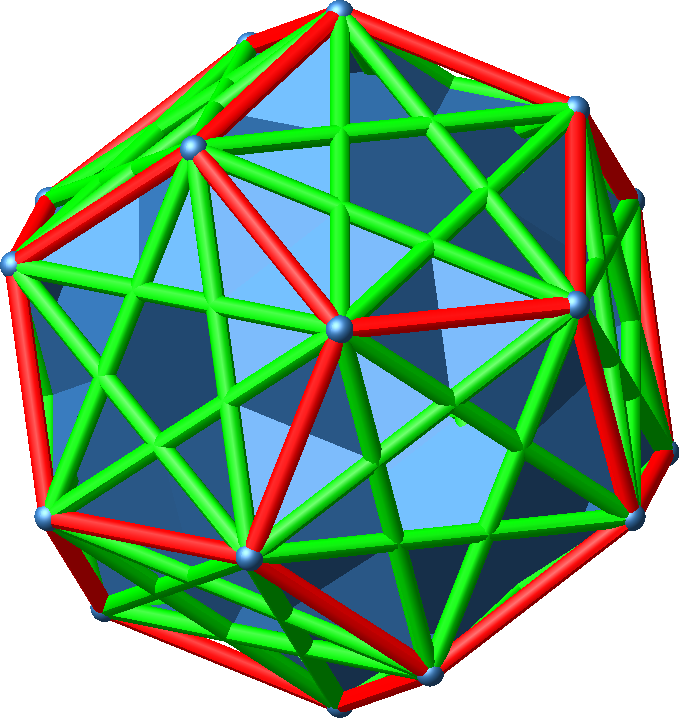
Abb. 4: Zwanzig gleichseitige Dreiecke

Allerdings sehen wir Kerben und Löcher. Die 20 Dreiecke bilden also nicht das klassische regelmäßige Ikosaeder. Die Figur ist kein geschlossenes Polyeder.

Die Abbildungen 5 und 6 zeigen die Situation ohne die stark markierten Ecken, Kanten und Seitenflächendiagonalen.

Abb. 5: Ikosaeder-Stern

Abb. 6: Rotierender Stern

In den Abbildungen 5 und 6 hat es Löcher mit Durchblick. Wir können diese mit Pentagrammen verschließen (Abb. 7 und 8).

Abb. 7: Pentagramme

Abb. 8: Stella vigintangula

Man kann sich den Stern vorstellen als Dodekaeder mit eingekerbten Kanten. Die Kerbleibungen sind kleinegleichseitige Dreiecke.

3 Topologie

Bauteile		#	Bemerkungen
Ecken	e	20	Das Dodekaeder hat 20 Ecken
Kanten	k	60	5 Diagonalen in jeder Seitenfläche des Dodekaeders
Seitenflächen	f	32	20 gleichseitige Dreiecke, 12 Pentagramme

Tab. 1: Bauteile

Es ist:

e – k + f = –8

Da wir Selbstdurchdringungen haben, gilt die Eulersche Polyederformel ( e – k + f = 2 ) nicht.

Literatur

Coxeter, H. S. M. / Du Val , P. / H.T. Flather, H. T. / Petrie, J. F. (1938): The Fifty-Nine Icosahedra. With 20 Plates and 9 Figures. New York: Springer 1938. ISBN 0-387-90770-X