Hans Walser, [20230737]

Ikosaeder

1 Worum es geht

Das Iksoaeder und seine Diagonalen. Einbau von Flächen

Bestandesaufnahme und Dokumantation

2 Koordinaten

Phi = Φ = (1+√5)/2 ≈ 1.618 (Goldener Schnitt).

Für die zwölf Eckpunkte und den Mittelpunkt verwenden wir folgende Koordinaten:

A[0] := [0, 0, 0]: (Mittelpunkt, Koordinatenursprung)

A[1] := [0, 1, 1/Phi]:

A[2] := [0, -1, 1/Phi]:

A[3] := [0, -1, -1/Phi]:

A[4] := [0, 1, -1/Phi]:

A[5] := [1/Phi, 0, 1]:

A[6] := [1/Phi, 0, -1]:

A[7] := [-1/Phi ,0, -1]:

A[8] := [-1/Phi, 0, 1]:

A[9] := [1, 1/Phi, 0]:

A[10] := [-1, 1/Phi, 0]:

A[11] := [-1, -1/Phi, 0]:

A[12] := [1, -1/Phi, 0]:

Die Abbildung 1 zeigt die Position der Punkte im Koordinatensystem.

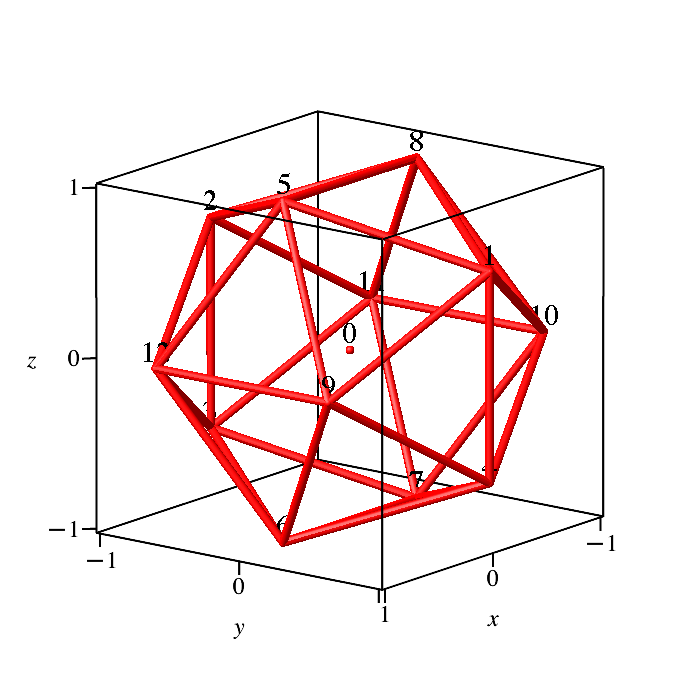
Abb. 1: Eckennummerierung

Die Ecken A[1] bis A[4], A[5] bis A[8] und A[9] bis A[12] bilden je ein Goldenes Rechteck (Abb. 2). Es gibt fünf solche Gerüste aus je drei Goldenen Rechtecken.

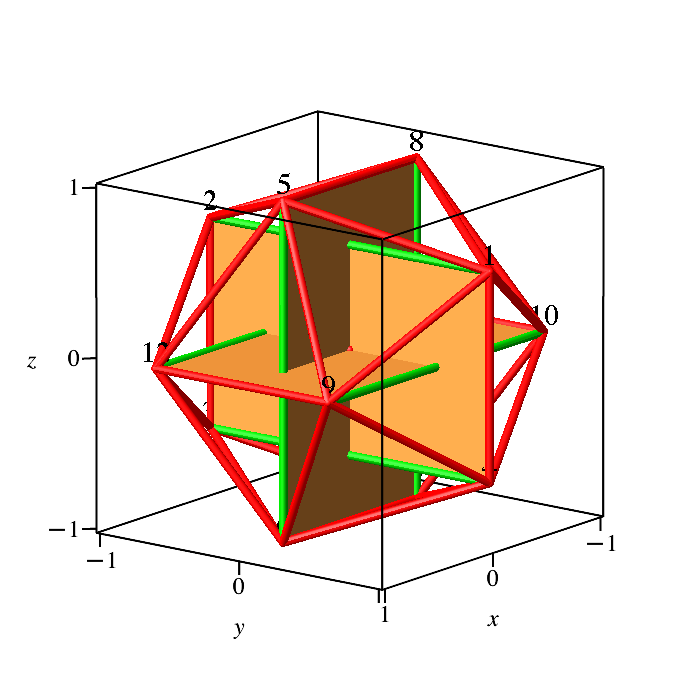
Abb. 2: Drei Goldene Rechtecke

Das Ikosaeder passt in einen Würfel (Abb. 3). Die Schmalseiten der Goldenen Rechtecke liegen auf den Würfelseiten.

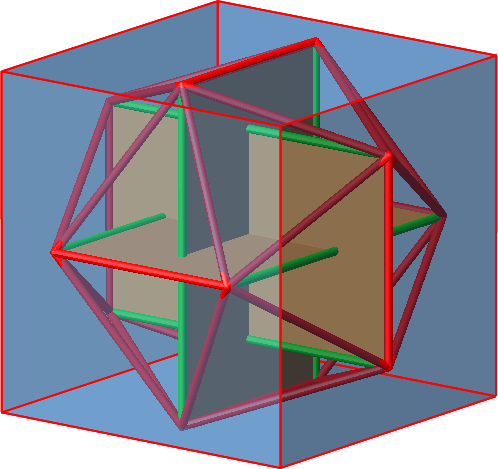
Abb. 3: Einpassen in den Würfel

3 Spezielle Positionen

Abb. 4.1: Auf Kante stehend

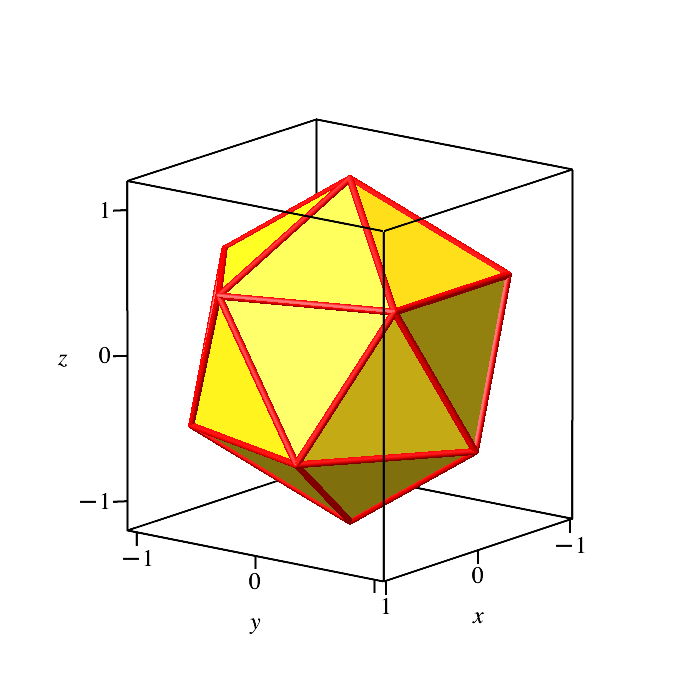
Abb. 4.2: Auf Ecke stehend

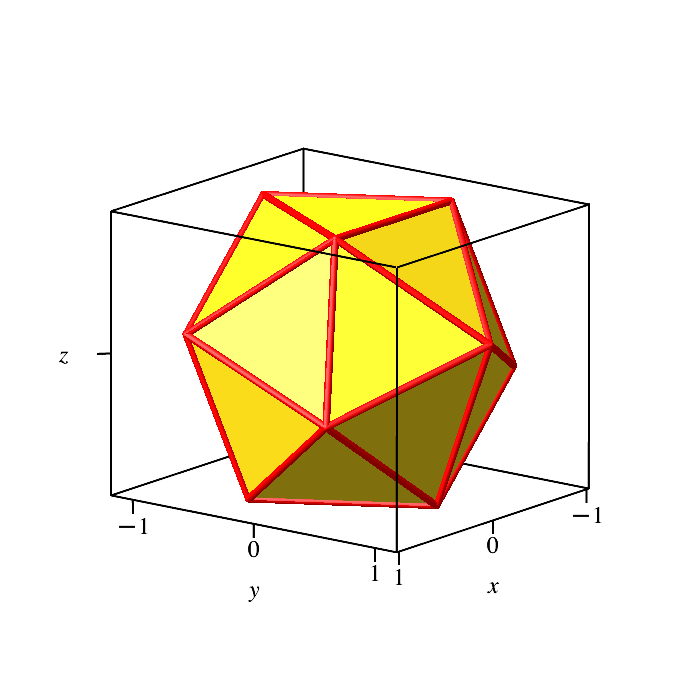
Abb. 4.3: Auf Seite stehend

4 Diagonalen

Die Abbildung 5.1 zeigt das Ikosaeder mit sämtlichen Diagonalen.

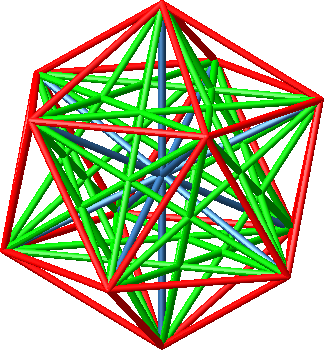
Abb. 5.1: Ikosaeder und Diagonalen

Die Hamming-Länge einer Diagonale bestimmen wir als die minimale Anzahl von Kanten auf dem Kantengerüst, um vom Anfangspunkt der Diagonale zum Endpunkt zu gelangen. Es handelt sich hier um die sogenannte Hamming-Distanz (Richard Wesley Hamming, 1915-1998). In unserem Kontext ist die Hamming-Länge immer eine natürliche Zahl. Die Kanten selber sind die „Diagonalen“ mit der Hamming-Länge eins. Die längsten Diagonalen (zwischen diametralen Punkten des Ikosaeders) haben die Hamming-Länge 3.

Die Tabelle 1 gibt eine Übersicht über die Diagonalenlängen. Dabei ist Φ der Goldene Schnitt, Φ ≈ 1.618033988. Die relative euklidische Länge ist bezogen auf die Kantenlänge.

Farbe
Hamming-Länge	1	2	3
Relative euklidische Länge	1	Φ	√(2 + Φ)
Relative euklidische Länge	1	1.618033988	1.902113032
Länge im Koordinatensystem	2/Φ	2	2/Φ*√(2 + Φ)
Länge im Koordinatensystem	1.236067978	2	2.351141010
Anzahl	30	30	6
Begriff	Kante	Raumdiagonale	Durchmesser

Tab. 1: Diagonalenlängen

Die Abbildung 5.2 zeigt die Diagonalen der Hamming-Seitenlänge 2.

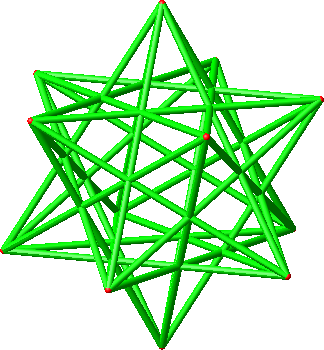
Abb. 5.2: Hamming-Seitenlänge 2

Die Abbildung 5.3 zeigt die Diagonalen der Hamming-Seitenlänge 3.

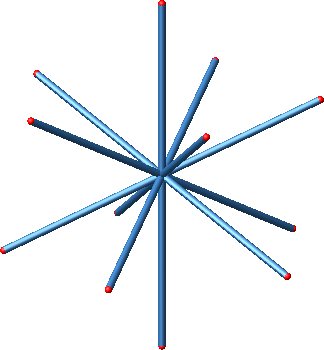
Abb. 5.2: Hamming-Seitenlänge 3

5 Einbau von Flächen

5.1 Gleichseitige Dreiecke

5.1.1 Hamming-Seitenlänge 1

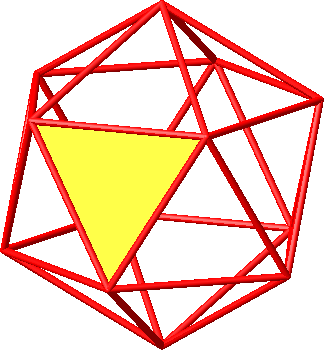
Abb. 6.1: Gleichseitiges Dreieck mit Hamming-Seitenlänge 1

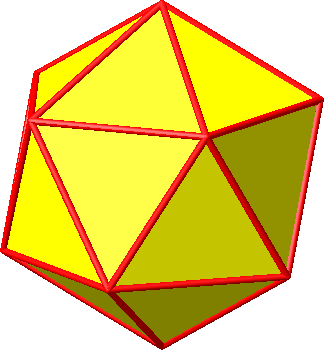
Abb. 6.2: Seitenflächen

Abb. 6.3: Ikosaeder mit Kanten

Abb. 6.4: Ikosaeder

5.1.2 Hamming-Seitenlänge 2

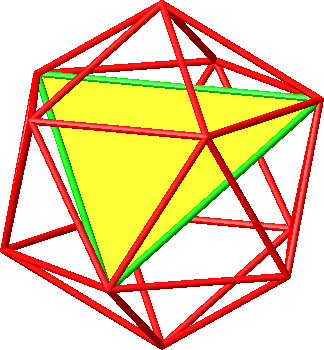
Abb. 7.1: Einzeldreieck

Der aus allen 20 solchen Dreiecken bestehende Stern heißt Großes Ikosaeder. Er ist einer der vier Kepler-Poinsot-Körper.

Abb. 7.2: Großes Ikosaeder

Abb. 7.3: Großes Ikosaeder

Abb. 7.4: Großes Ikosaeder

5.2 Regelmäßige Fünfecke

Abb. 8.1: Einzelfünfeck

Das aus allen 12 solchen Fünfecken bestehende Polyeder heißt Großes Dodekaeder. Es ist einer der vier Kepler-Poinsot-Körper.

Abb. 8.2: Großes Dodekaeder

Abb. 8.3: Großes Dodekaeder

Abb. 8.4: Großes Dodekaeder

5.3 Pentagramme

Abb. 9.1: Einzelpentagrqmm

Das aus allen 12 solchen Pentagrammen bestehende Polyeder heißt Dodekaeder-Stern. Es ist einer der vier Kepler-Poinsot-Körper.

Abb. 9.2: Dodekaeder-Stern

Abb. 9.3: Dodekaeder-Stern

Abb. 9.4: Dodekaeder-Stern

5.4 Goldene Rechtecke

Die Ebenen der Goldenen Rechtecke sind auch die Symmetrieebenen des Ikosaeders. Es hat 15 Goldene Rechtecke und damit 15 Symmetrieebenen im Ikosaeder.

Abb. 10.1: Einzelnes Goldenes Rechteck

Abb. 10.2: Drei paarweise rechtwinklige Goldene Rechtecke

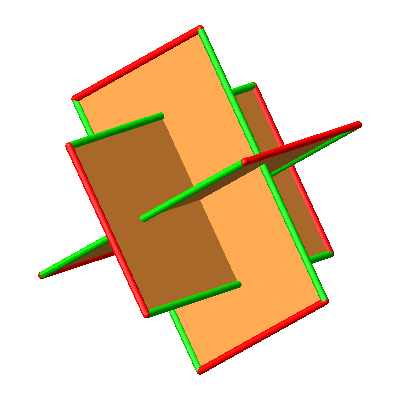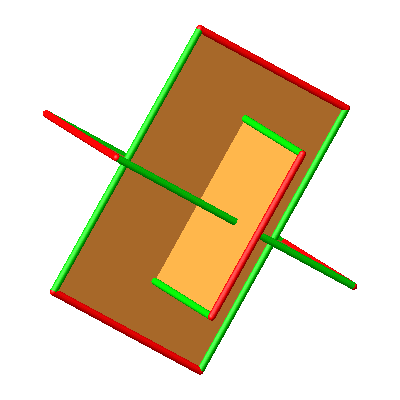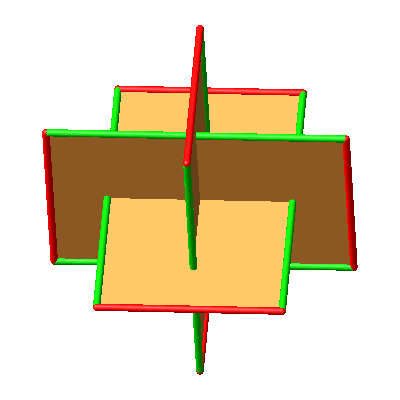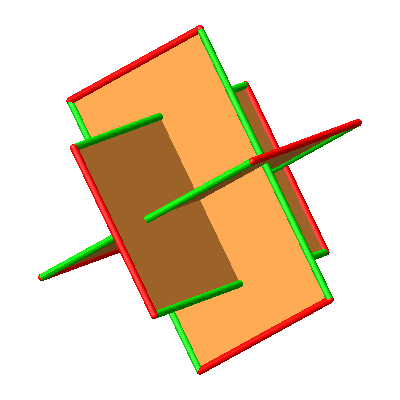
Abb. 10.3: Drei paarweise rechtwinklige Goldene Rechtecke

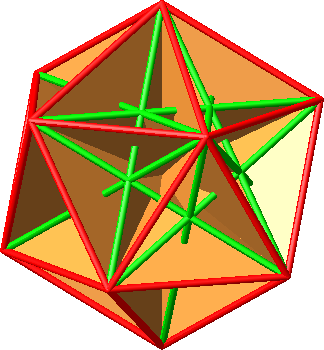
Abb. 10.4: Alle Goldenen Rechtecke

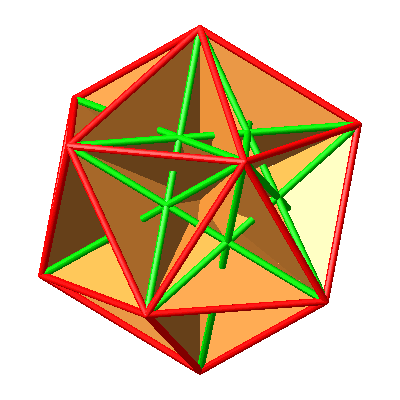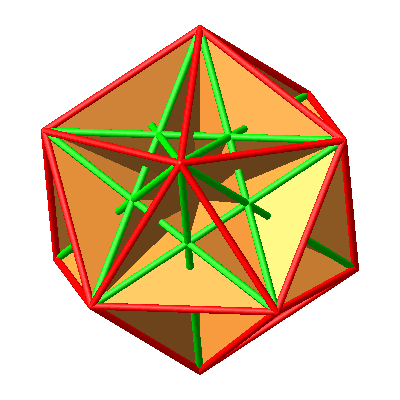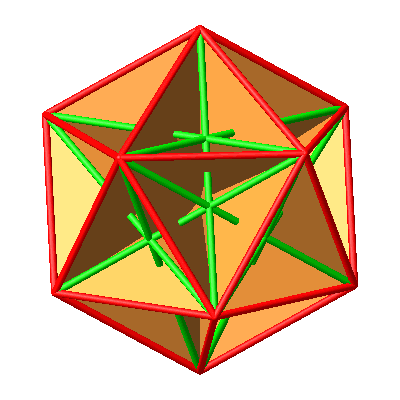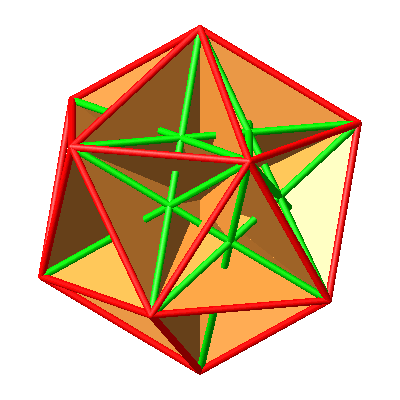
Abb. 10.5: Alle Goldenen Rechtecke

Abb. 10.6: Alle Goldenen Rechtecke

5.5 Gleichschenklige Dreiecke

Wir zerlegen die Goldenen Rechtecke mit den Diagonalen in gleichschenklige Dreiecke (Abb. 11). Damit kommt der Mittelpunkt ins Spiel.

Abb. 11: Zerlegung in gleichschenklige Dreiecke

5.5.1 Spitze gleichschenklige Dreiecke

Es gibt 30 spitze gleichschenklige Dreiecke, je eins pro Kante.

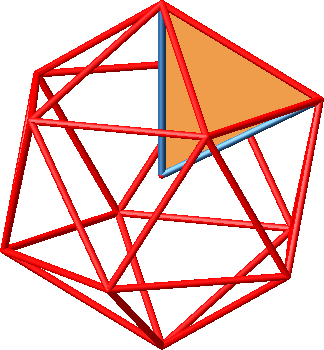
Abb. 12.1: Einzeldreieck

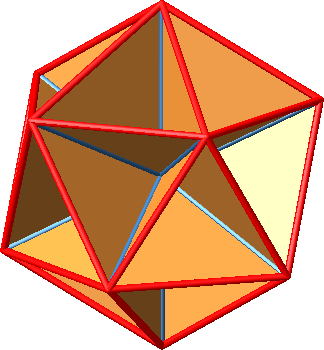
Abb. 12.2: Alle Dreiecke

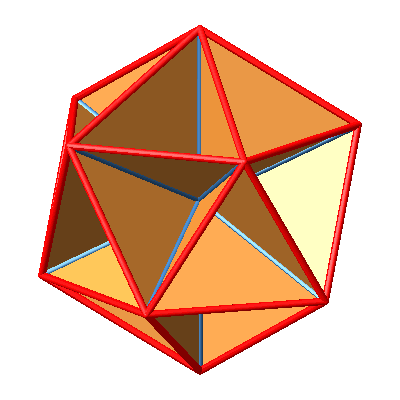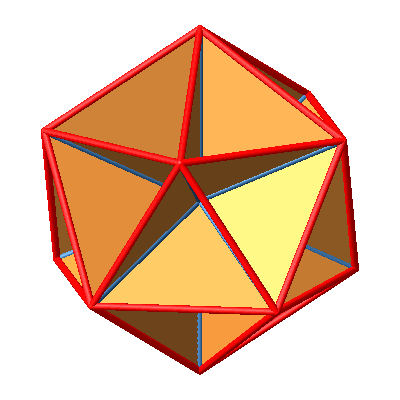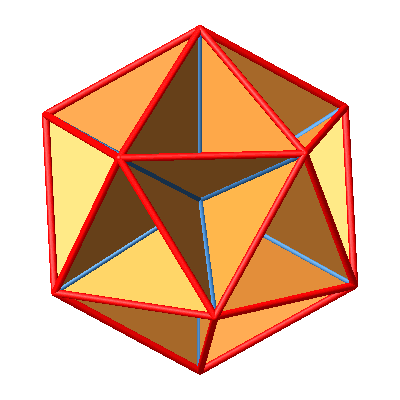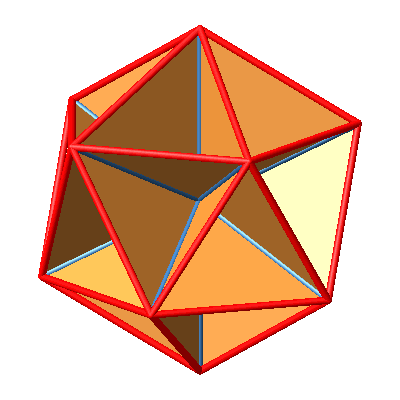
Abb. 12.3: Alle Dreiecke

Abb. 12.4: Alle Dreiecke

5.5.2 Stumpfe gleichschenklige Dreiecke

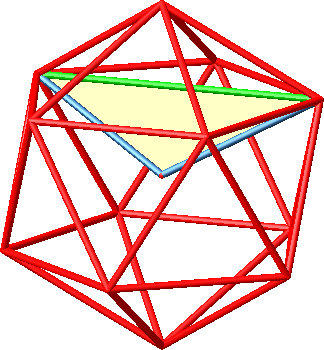
Abb. 13.1: Einzeldreieck

Abb. 13.2: Alle Dreiecke

Abb. 13.3: Alle Dreiecke

Abb. 13:4: Alle Dreiecke

6 Die vier Kepler-Poinsot-Körper

Johannes Kepler, 1571-1630

Louis Poinsot, 1777-1859

6.1 Dodekaeder-Stern

Der Dodekaeder-Stern besteht aus einem Dodekaeder mit zwölf aufgesetzten Fünfkantpyramiden. Die konvexe Hülle (rote Kanten) ist ein Ikosaeder.

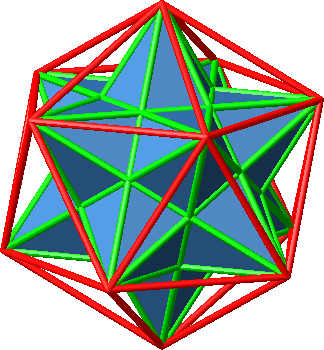
Abb. 14: Dodekaeder-Stern

6.2 Ikosaeder-Stern

Der Ikosaeder-Stern besteht aus einem Ikosaeder mit 20 aufgesetzten Dreikantpyramiden. Die konvexe Hülle (rote Kanten) ist ein Dodekaeder.

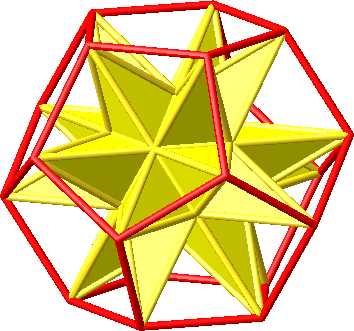
Abb. 15: Ikosaeder-Stern

6.3 Großes Dodekaeder

Die zwölf Seitenflächen des Großen Dodekaeders sind regelmäßige Fünfecke.

Abb. 16: Großes Dodekaeder

6.4 Großes Ikosaeder

Die 20 Seitenflächen des Großen Ikosaeders sind gleichseitige Dreiecke.

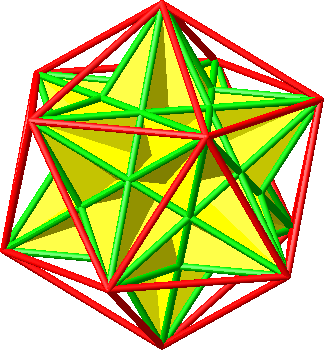
Abb. 17: Großes Ikosaeder

Weblinks

Hans Walser: Dodekaeder

http://www.walser-h-m.ch/hans/Miniaturen/D/Dodekaeder3/Dodekaeder3.html