Hans Walser, [20230803]

Ikosaeder

1 Worum es geht

Kinematische Spielerei mit einem in der Regel nicht regelmäßigen Ikosaeder.

2 Grundidee

Zum Parameterwert t arbeiten wir mit den zwölf Punkten mit den Koordinaten:

[±1,±t,0], [0,±1,±t], [±t,0,±1]

Beispiele:

Für t = 0 erhalten wir die Ecken des Oktaeders (Abb. 1). Je zwei der zwölf Punkte fallen zusammen.

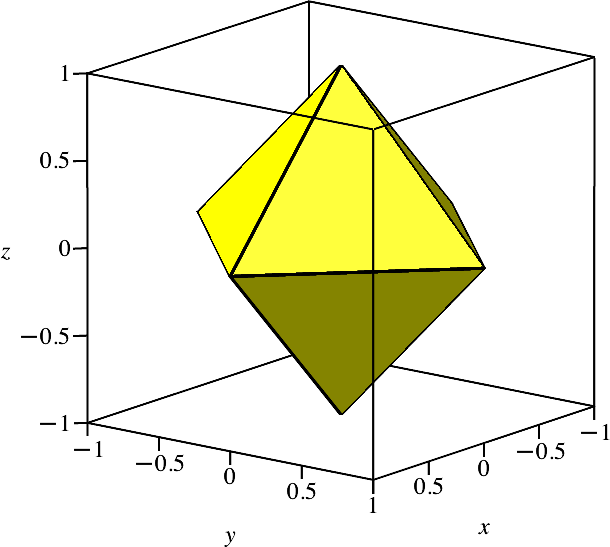
Abb. 1: Oktaeder

Im folgenden Beispiel verwenden wir den Goldenen Schnitt Φ = (1+√5)/2 ≈ 1.618. Bei t = 1/Φ ≈ 0.618 ergeben sich die Ecken für das regelmäßige Ikosaeder (Abb. 2).

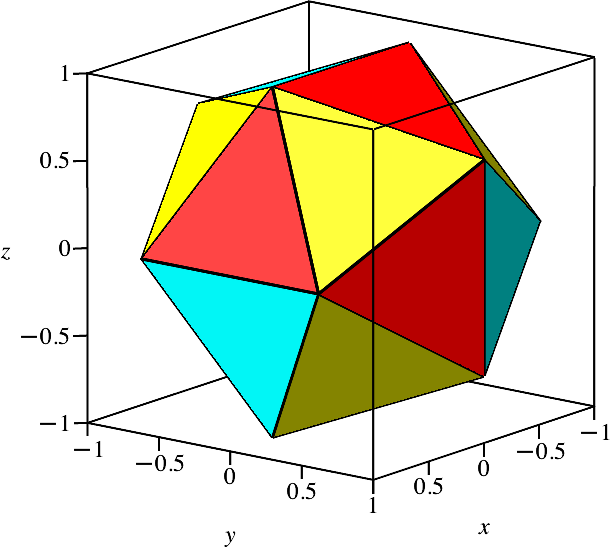
Abb. 2: Regelmäßiges Ikosaeder

Für t = 1 erhalten wir die Ecken eines Kuboktaeder (Abb. 3).

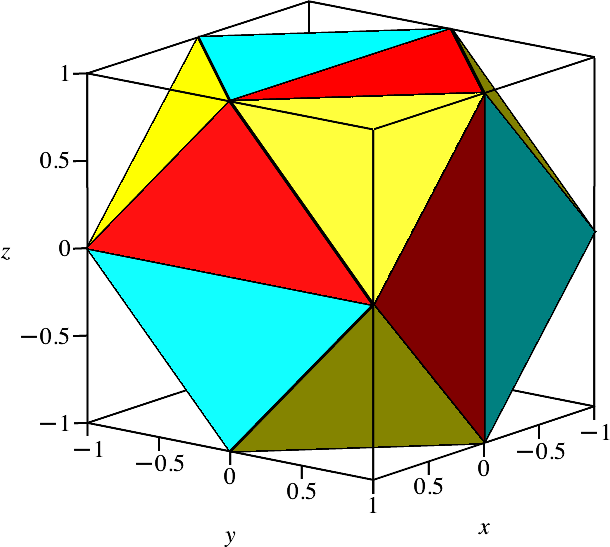
Abb. 3: Kuboktaeder

3 Normierung

Die gelben Dreiecke sind immer gleichseitig, die Seitenlängen variieren aber in den Beispielen. Beim Oktaeder und beim Kuboktaeder haben wir die Seitenlängen √2/2, beim Ikosaeder ist die Seitenlänge etwas kleiner. Um dies zu vermeiden, skalieren wir die Figuren so, dass die Seitenlängen der gelben Dreiecke einheitlich √2/2 werden. Das Ikosaeder wird dann etwas größer (Abb. 4). Es passt nicht mehr in den Basiswürfel mit der Kantenlänge 2.

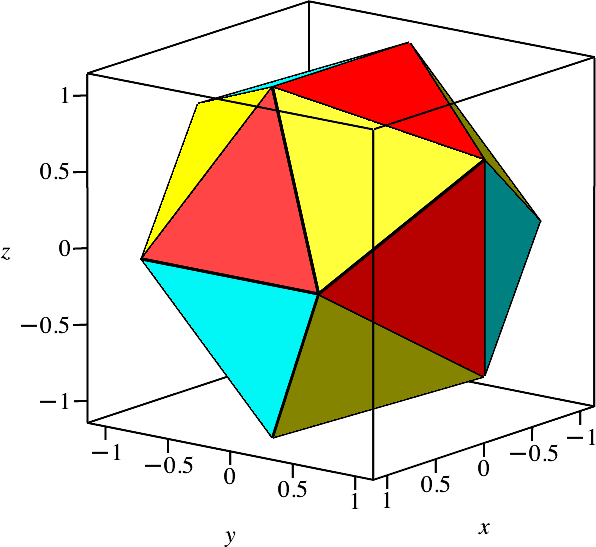
Abb. 4: Normiertes Ikosaeder

4 Vom Kuboktaeder zum Oktaeder

Die Abbildung 5 zeigt den Übergang vom Oktaeder via Ikosaeder zum Kuboktaeder und zurück. Die gelben gleichseitigen Dreiecke drehen. Ihr Abstand vom Mittelpunkt variiert beim Drehen.

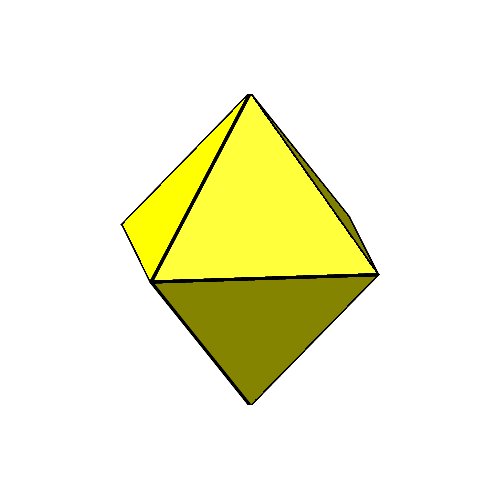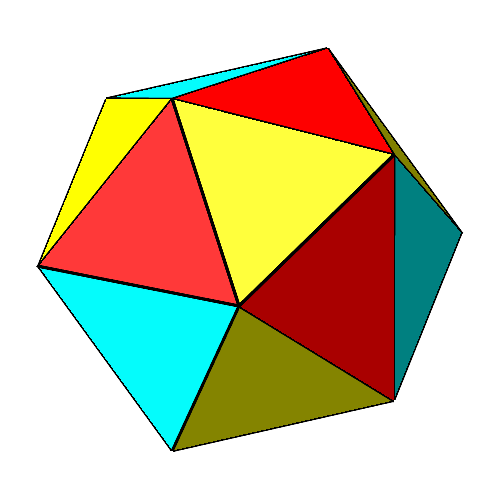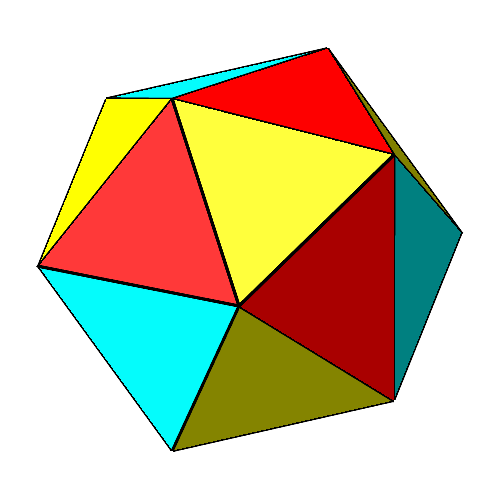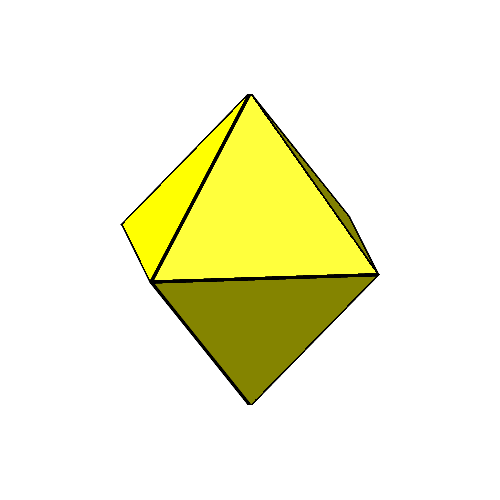
Abb. 5: Übergang

5 Weiterdrehen

Die Frage ist nun, das geschieht, wenn wir die gelben gleichseitigen Dreiecke weiterdrehen lassen(Abb. 6). Wie sehen mehrere Stationen.

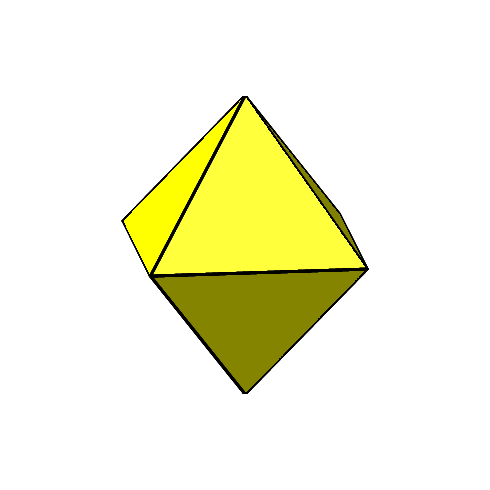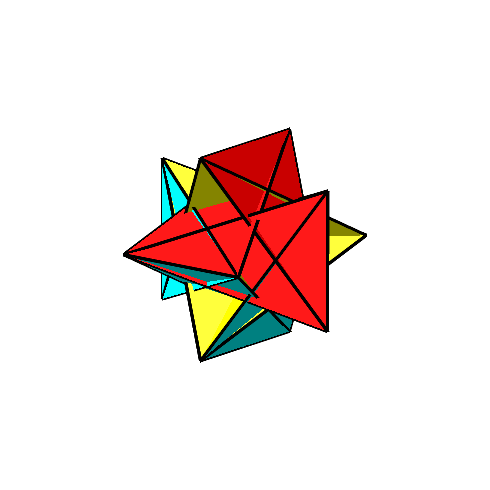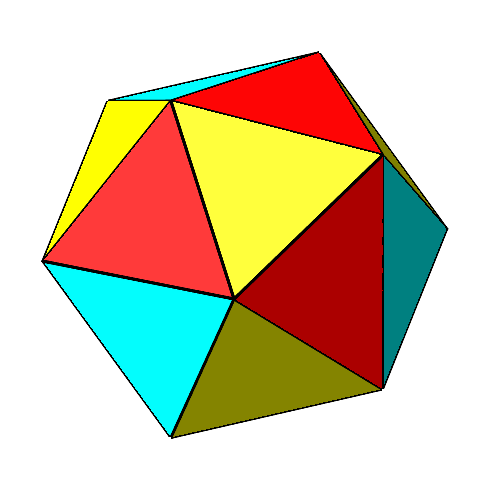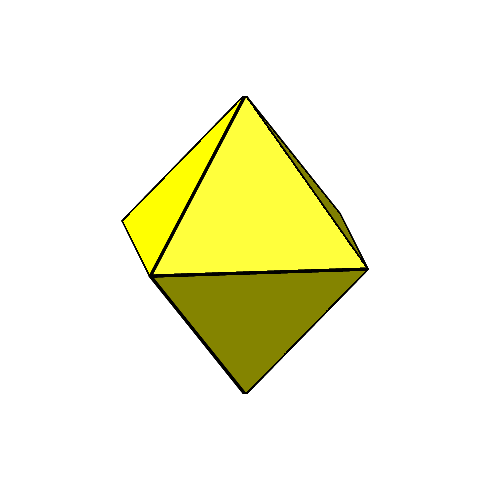
Abb. 6: Weiterdrehen

6 Stationen

Wir haben die folgenden Stationen.

6.1 Oktaeder

Für t → – ∞ ergibt sich ein Oktaeder.

6.2 Großes Ikosaeder

Für t = – Φ erhalten wir das sogenannte große Ikosaeder (Abb. 7 und 8). Es besteht wie das gewöhnliche Ikosaeder aus 20 gleichseitigen Dreiecken. Diese durchschneiden sich aber gegenseitig.

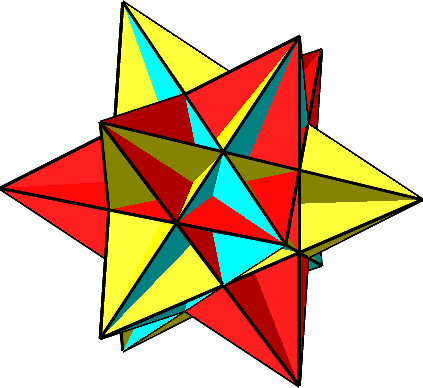
Abb. 7: Großes Ikosaeder

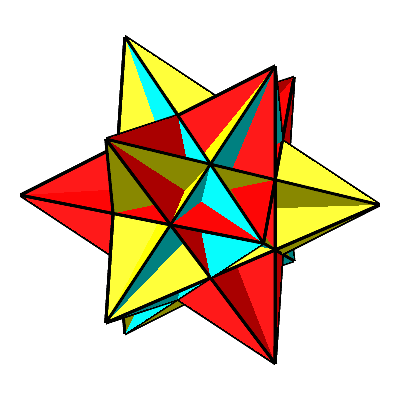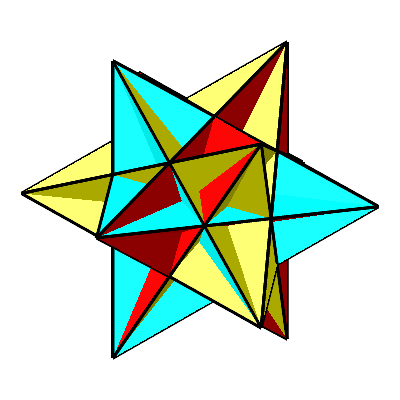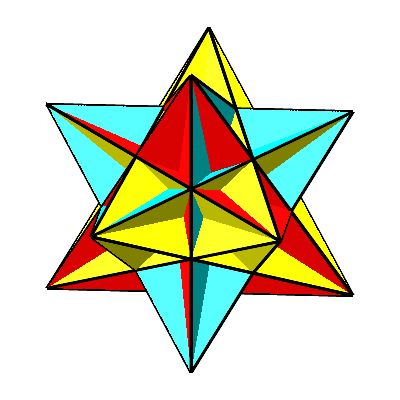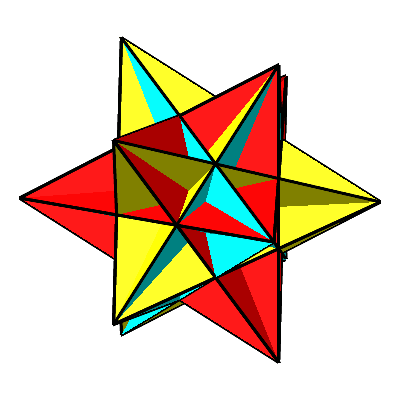
Abb. 8: Großes Ikosaeder

6.3 Unbekannte Figur

Für t = –1 ergibt sich eine mir unbekannte Figur (Abb. 9 und 10). Die Ecken liegen wie beim Kuboktaeder auf den Kantenmitten eines Würfels.

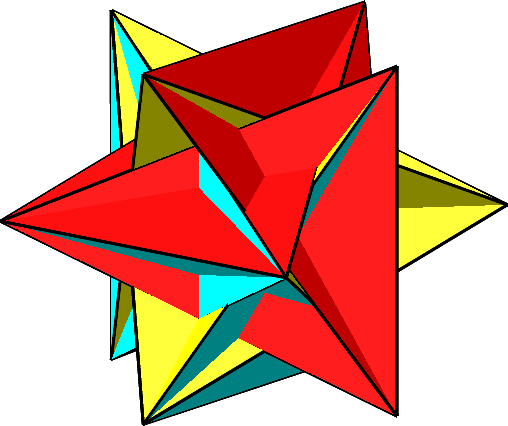
Abb. 9: Unbekannte Figur

Abb. 10: Unbekannte Figur

6.4 Doppelaxt

Für t = –1/ Φ ergibt sich die Doppelaxt (Abb. 11 und 12). Ihre konvexe Hülle ist ein regelmäßiges Ikosaeder. Die gelben Dreiecke sind (gemäß Konstruktion) gleichseitig. Die roten und die blauen Dreiecke sind gleichschenklig. Die Schenkellänge ist gleich der Seitenlänge der gleichseitigen Dreiecke. Die Basis ist der Minor dazu, das heißt mit dem Faktor 1/ Φ verkürzt. Die Basiswinkel sind 72°. Es handelt sich um sogenannte spitze Goldene Dreiecke.

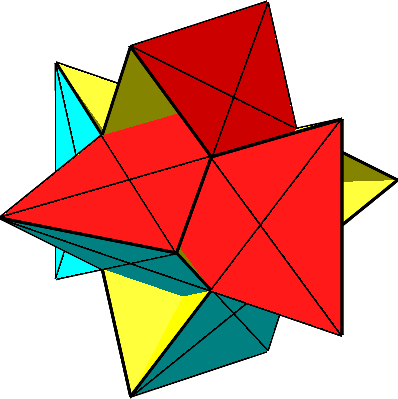
Abb. 11: Doppelaxt

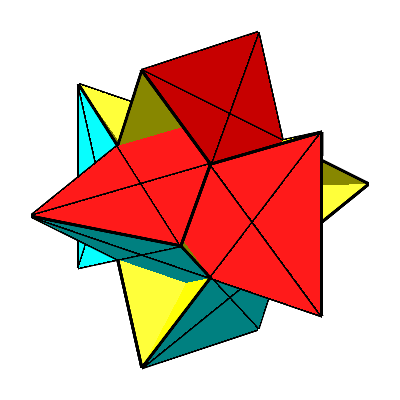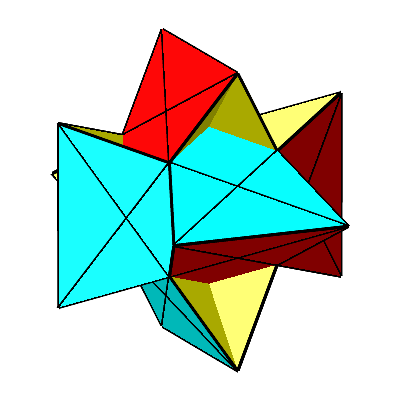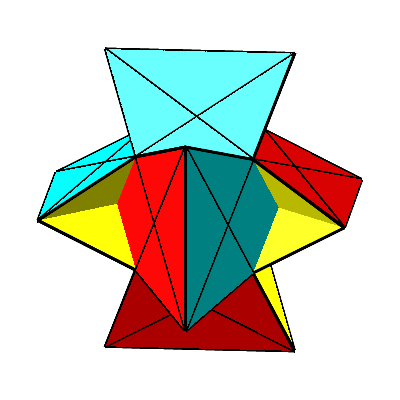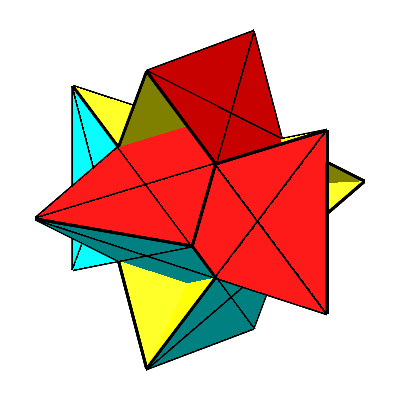
Abb. 12: Doppelaxt

6.5 Oktaeder

Für t = 0 erhalten wir die Ecken des Oktaeders (Abb. 3). Je zwei der zwölf Punkte fallen zusammen.

6.6 Regelmäßiges Ikosaeder

Für t = 1/ Φ erhalten wir das regelmäßige Ikosaeder (Abb. 2 und 4).

6.7 Kuboktaeder

Für t = 1 ergibt sich das Kuboktaeder (Abb. 3).

6.8 Gekerbtes Ikosaeder

Für t = Φ ergibt sich das gekerbte Ikosaeder (Abb. 13 und 14). Seine konvexe Hülle ist ein regelmäßiges Ikosaeder. Die gelben Dreiecke sind gleichseitig. Die roten und die blauen Dreiecke sind gleichschenklig. Die Schenkellänge ist gleich der Seitenlänge der gleichseitigen Dreiecke. Die Basis ist der Major dazu, das heißt mit dem Faktor Φ vergrößert. Die Basiswinkel sind 36°. Es handelt sich um sogenannte stumpfe Goldene Dreiecke.

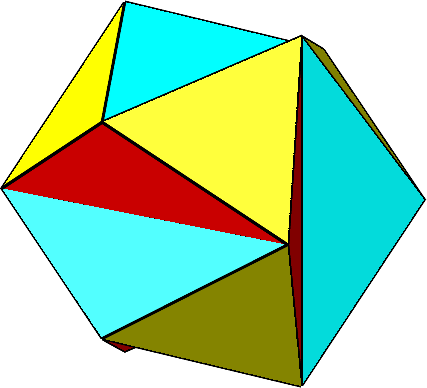
Abb. 13: Gekerbtes Ikosaeder

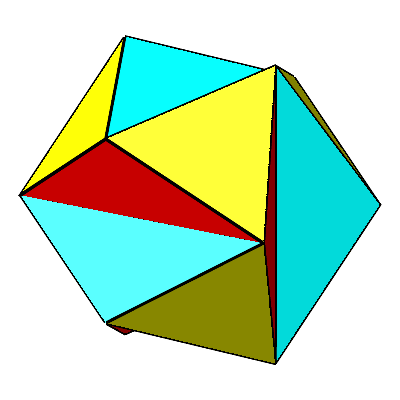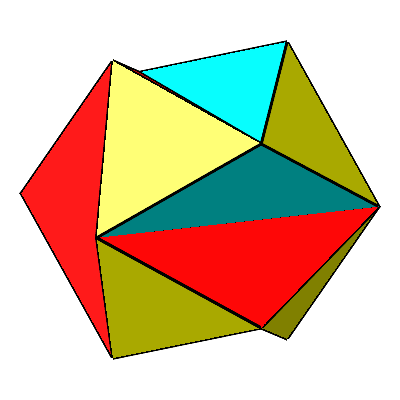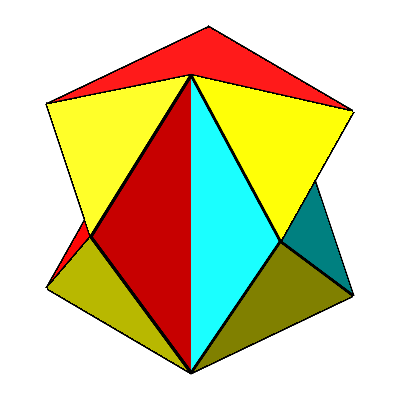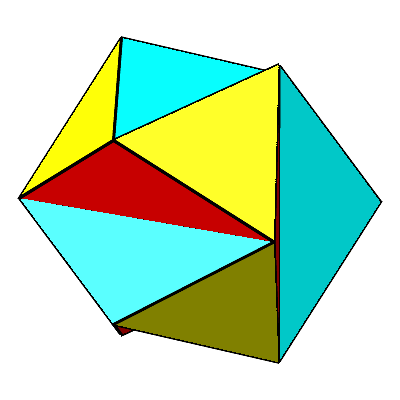
Abb. 14: Gekerbtes Ikosaeder

6.9 Oktaeder

Für t → ∞ ergibt sich ein Oktaeder. In der Abbildung 6 sind das erste und das letzte Oktaeder identifiziert, so dass sich ein Rundlauf ergibt.

Weblinks

Hans Walser: Ikosaeder

http://www.walser-h-m.ch/hans/Miniaturen/I/Ikosaeder2/Ikosaeder2.html