Hans Walser, [20220430]

Inkreis von pythagoreischen Dreiecken

1 Worum geht es?

Parametrisierung

2 Disposition

Mit den üblichen Parametern u und v mit u > v und gcd(u,v) = 1 und modp(u-v, 2) = 1 definieren wir:

a := u^2 - v^2:

b := 2*u*v:

c := u^2 + v^2:

A := [a,b]:

B := [0,0]:

C := [a,0]:

3 Mittelpunkt und Radius

Für den Mittelpunkt I und den Radius r des Inkreises ergibt sich damit:

I := [u*(u-v), v*(u-v)]:

r := v*(u-v):

Die Tabelle 1 gibt die ersten Beispiele. Die Inkreisradien sind ganzzahlig. Sie können mehrfach vorkommen.

Nr.	u	v	a	b	c	I	r	Bemerkungen
1	2	1	3	4	5	[2, 1]	1	Lehrerdreieck
2	3	2	5	12	13	[3, 2]	2	Indisches Dreieck
3	4	1	15	8	17	[12, 3]	3
4	4	3	7	24	25	[4, 3]	3
5	5	2	21	20	29	[15, 6]	6
6	5	4	9	40	41	[5, 4]	4
7	6	1	35	12	37	[30, 5]	5
8	6	5	11	60	61	[6, 5]	5
9	7	2	45	28	53	[35, 10]	10
10	7	4	33	56	65	[21, 12]	12
11	7	6	13	84	85	[7, 6]	6
12	8	1	63	16	65	[56, 7]	7
13	8	3	55	48	73	[40, 15]	15
14	8	5	39	80	89	[24, 15]	15
15	8	7	15	112	113	[8, 7]	7
16	9	2	77	36	85	[63, 14]	14
17	9	4	65	72	97	[45, 20]	20
18	9	8	17	144	145	[9, 8]	8
19	10	1	99	20	101	[90, 9]	9
20	10	3	91	60	109	[70, 21]	21
21	10	7	51	140	149	[30, 21]	21
22	10	9	19	180	181	[10, 9]	9

Tab. 1: Beispiele

4 Beispiele

Nr. 1, Lehrerdreieck (Abb. 1)

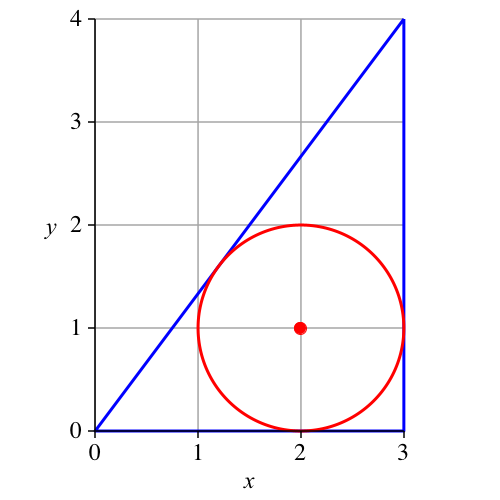
Abb. 1: Lehrerdreieck

Nr. 2: Indisches Dreieck (Abb. 2).

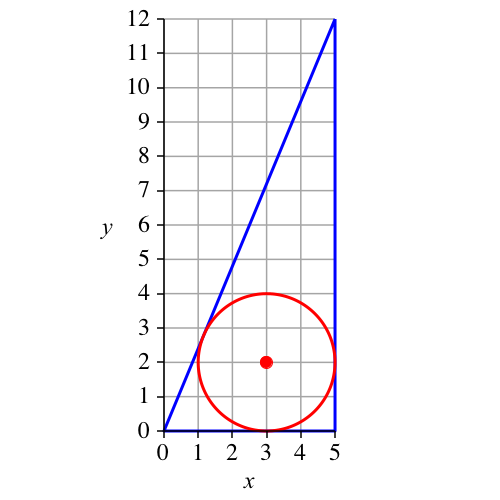
Abb. 2: Indisches Dreieck

Nr. 3 und Nr. 4: Inkreisradius = 3

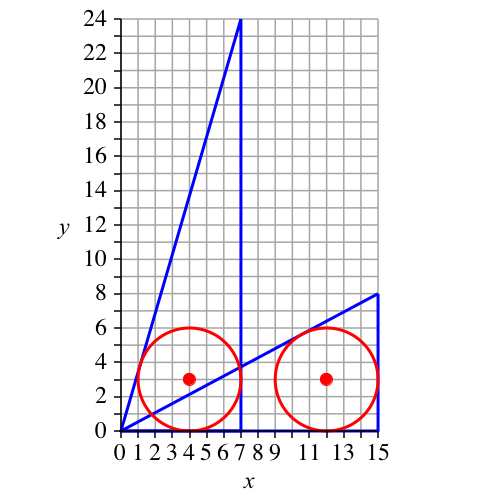
Abb. 3: Gleicher Inkreisradius

Weblinks

Hans Walser: Inkreis

http://www.walser-h-m.ch/hans/Miniaturen/I/Inkreis/Inkreis.htm

Hans Walser: Inkreise

http://www.walser-h-m.ch/hans/Miniaturen/I/Inkreise/Inkreise.htm

Hans Walser: Inkreise von Bogendreiecken

http://www.walser-h-m.ch/hans/Miniaturen/I/Inkreise_Bogendreiecke/Inkreise_Bogendreiecke.htm

Hans Walser: Inkreisradien

http://www.walser-h-m.ch/hans/Miniaturen/I/Inkreisradien/Inkreisradien.htm