1 Worum geht es?

Spielerei um den Inkreis. Kopunktale Geraden. Siebenpunktekreis. Sechspunktekegelschnitt.

2 Inkreismittelpunkt

In einem beliebigen nicht regelmäßigen Dreieck spiegeln wir den Inkreismittelpunkt an jeder Dreiecksseite (Abb. 1).

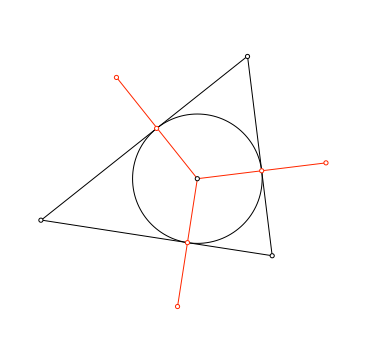
Abb. 1: Inkreismittelpunkt herausspiegeln.

Die Verbindungsgeraden der herausgespiegelten Punkte mit den gegenüberliegenden Dreiecksecken schneiden sich in einem Punkt (Abb. 2). Es handelt sich hier um einen Sonderfall des Satzes von Jacobi (Walser 1991, Walser 2012, S. 150-153).

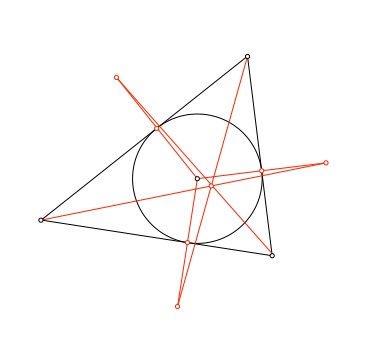
Abb. 2: Schnittpunkt

3 Eine Hyperbel

Wir legen den Kegelschnitt durch diesen Schnittpunkt, den Inkreismittelpunkt und die drei Dreiecksecken (Abb. 3).

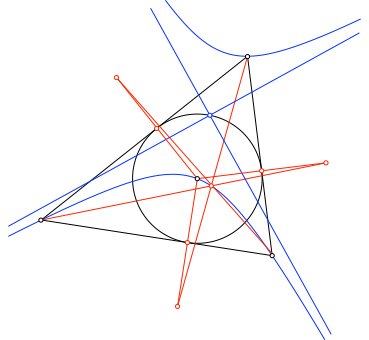
Abb. 3: Gleichseitige Hyperbel

Der Kegelschnitt ist eine gleichseitige Hyperbel, die Asymptoten sind orthogonal. Der Mittelpunkt der Hyperbel liegt auf dem Umkreis. Erhärtung mit DGS.

4 Höhenschnittpunkt

Der Höhenschnittpunkt des Dreieckes liegt ebenfalls auf der Hyperbel (Abb. 4). Die Hyperbel ist also ein Sechspunktekegelschnitt (DGS).

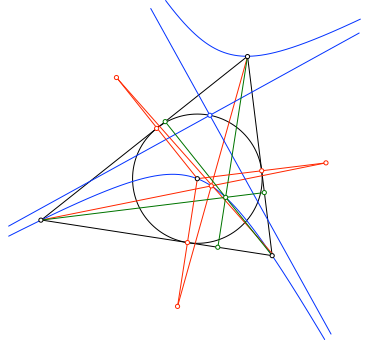
Abb. 4: Höhenschnittpunkt

5 Umkreis

Nun spiegeln wir den Höhenschnittpunkt an den Dreieckseiten (Abb. 5). Die Spiegelpunkte liegen auf dem Umkreis des Dreieckes. Dies kann mit Winkelüberlegungen gezeigt werden. Der Umkreis ist also (vorerst) ein Sechspunktekreis.

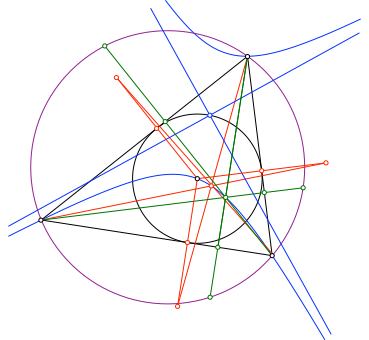
Abb. 5: Umkreis

6 Noch ein Schnittpunkt

Wir legen je eine Gerade durch die auf der gleichen Dreiecksseite herausgespiegelten Inkreismittelpunkt und Höhenschnittpunkt (Abb. 6). Die drei Geraden sind kopunktal. Der Schnittpunkt liegt auf dem Umkreis. Dieser ist nun ein Siebenpunktekreis (DGS).

Abb. 6: Noch ein Schnittpunkt

Weblinks

Hans Walser: Schnittpunkte 101-200

http://www.walser-h-m.ch/hans/Schnittpunkte/Schnittpunkte_101-200.pdf

Literatur

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0

Walser, Hans (1991): Ein Schnittpunktsatz. Praxis der Mathematik (33), 1991, 70-71.