Hans Walser, [20240613]

Inkreis und Umkreis

1 Worum es geht

Schließungsfigur der Periodenlänge 3

Satz von Poncelet

2 Inkreis und Umkreis

Zu einem beliebigen Dreieck zeichnen wir den Inkreis und den Umkreis (Abb. 1).

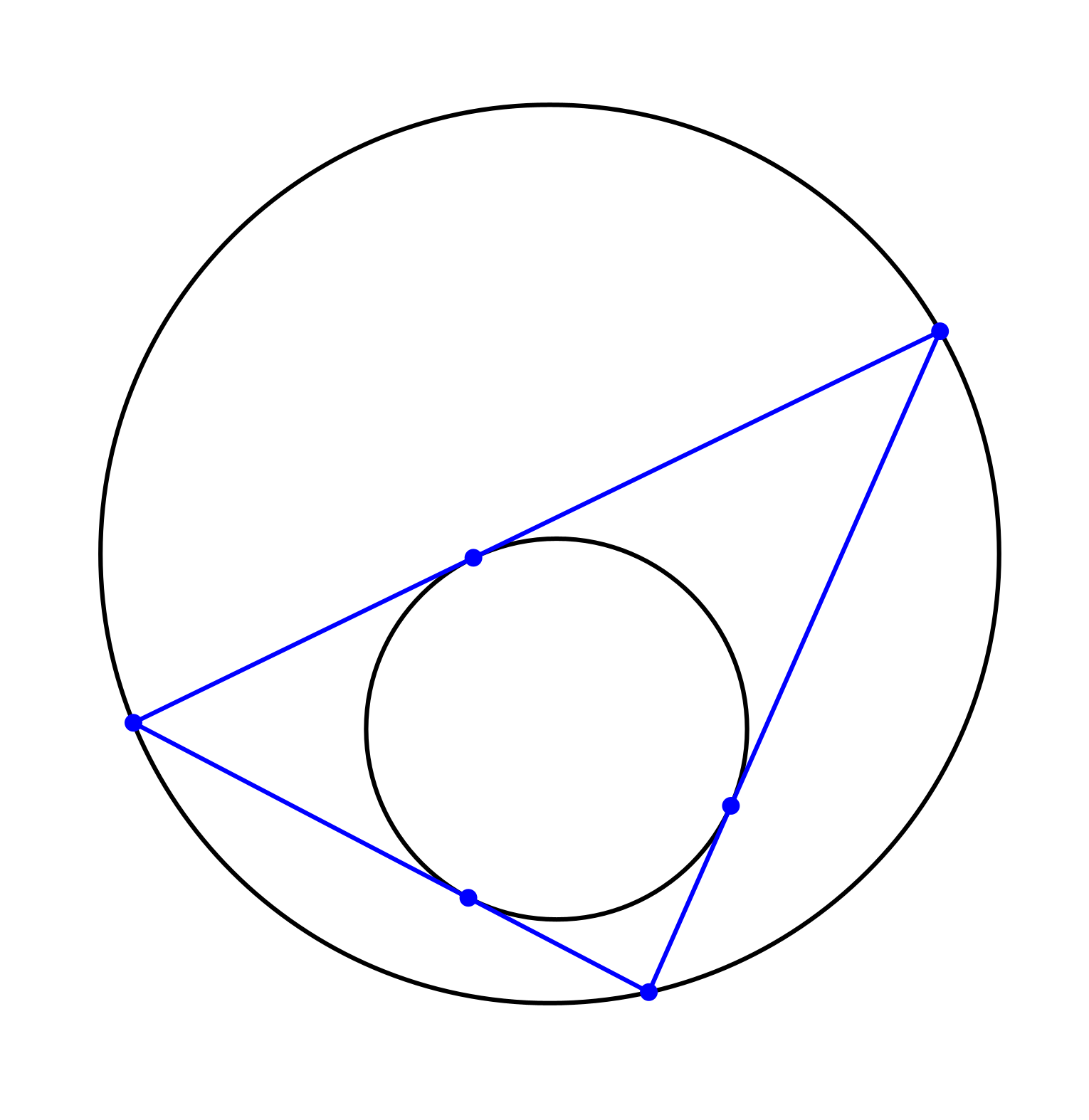
Abb. 1: Inkreis und Umkreis

3 Schließungsfigur

Auf dem Umkreis wählen wir einen beliebigen Startpunkt P₀ (Abb. 2).

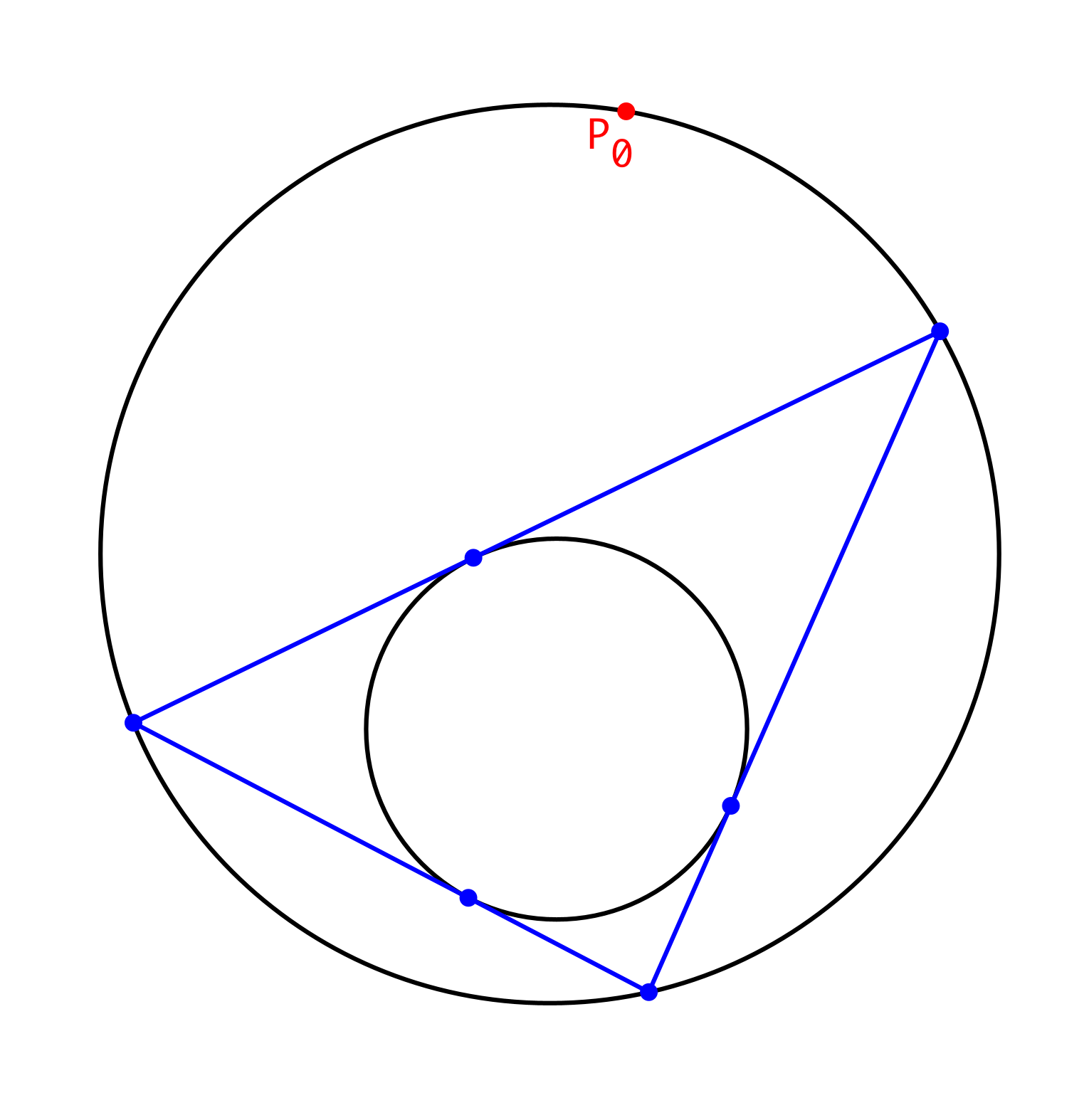
Abb. 2: Startpunkt

Von P₀ aus zeichnen wir diejenige Tangente an den Inkreis, welche von P₀ aus gesehen auf der rechten Seite des Inkreises vorbeigeht (Abb. 3). Den zweiten Schnittpunkt dieser Tangente mit dem Umkreis bezeichnen wir mit P₁.

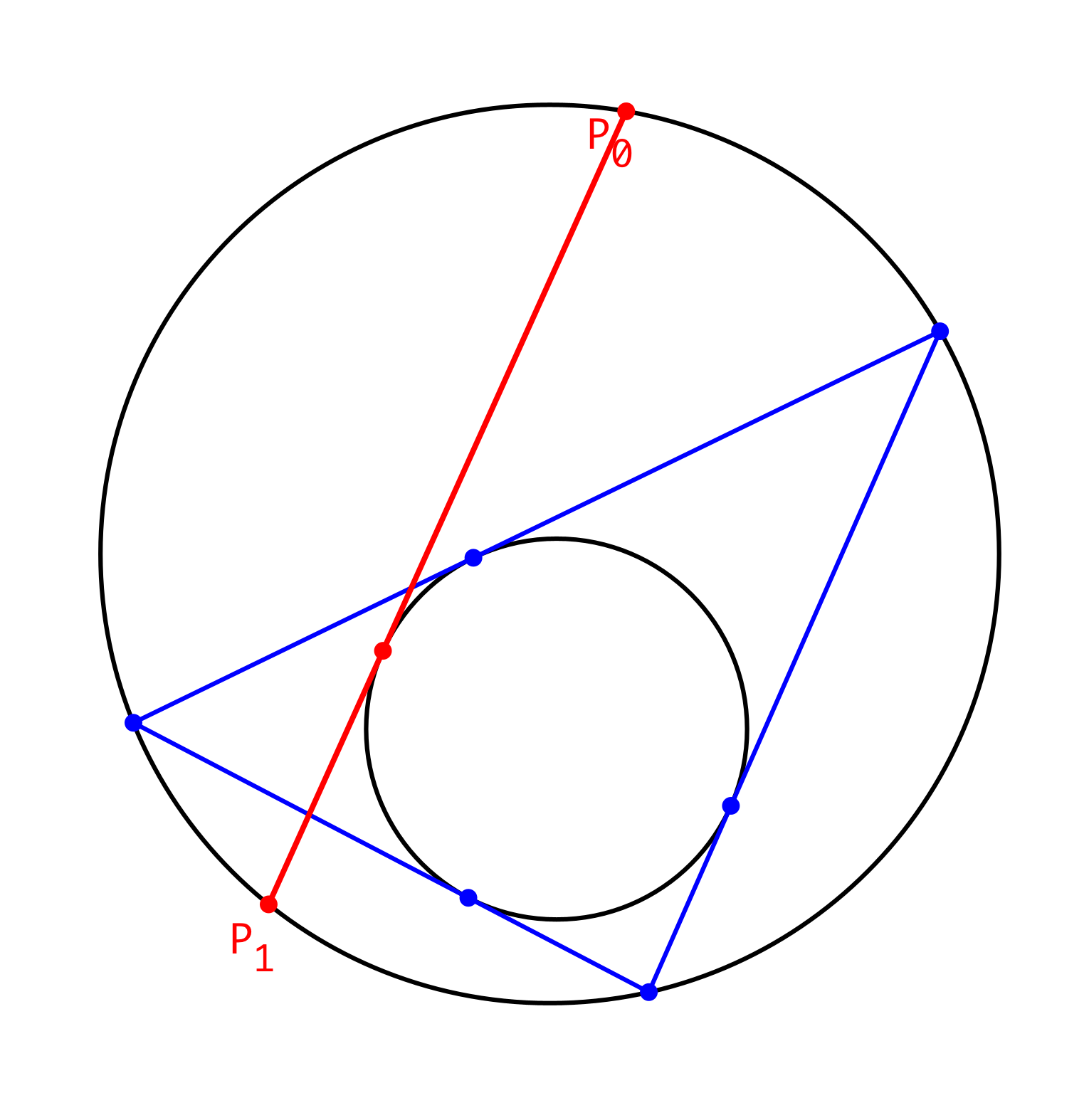
Abb. 3: Erster Schritt

Von P₁ aus zeichnen wir wiederum die Tangente rechts am Inkreis vorbei und erhalten als zweiten Schnittpunkt P₂ (Abb. 4).

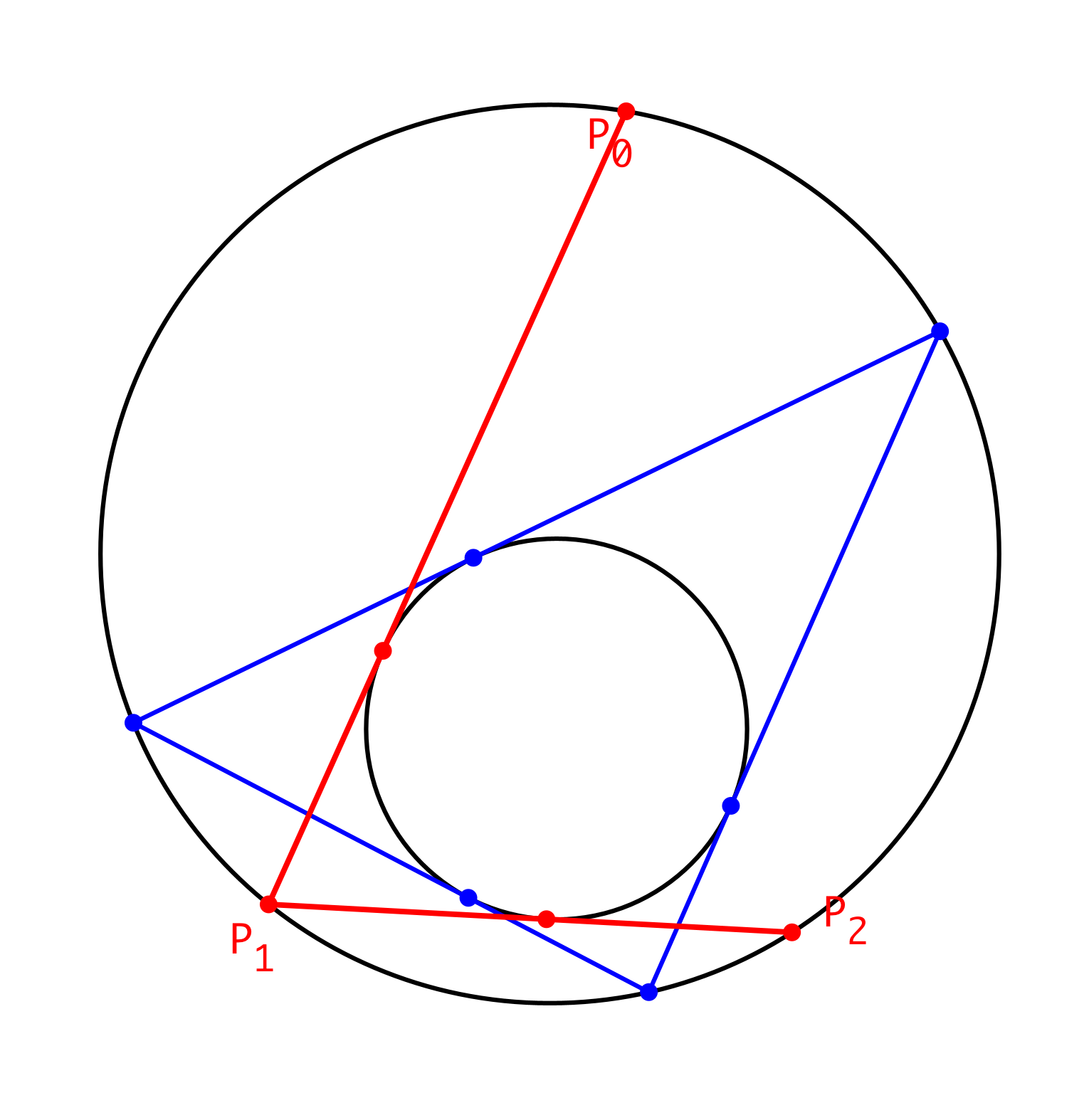
Abb. 4: Zweiter Schritt

Beim nächsten Schritt wird P₃ = P₀ (Abb. 5). Wir kommen zum Startpunkt zurück und haben daher eine Schließungsfigur.

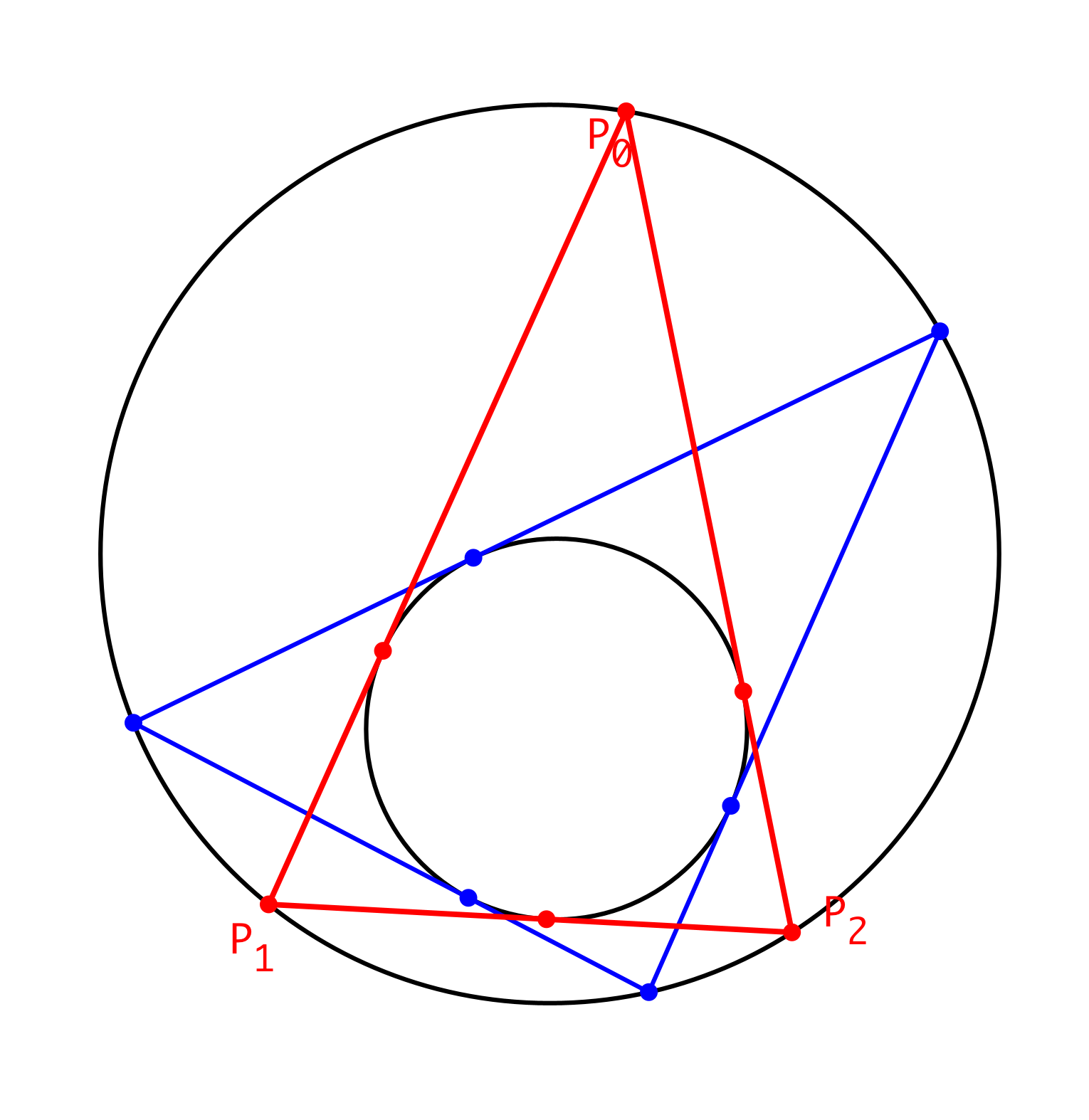
Abb. 5: Schließungsfigur

Die Schließungseigenschaft gilt unabhängig von der Wahl des Startpunktes P₀ auf dem Umkreis (Abb. 6).

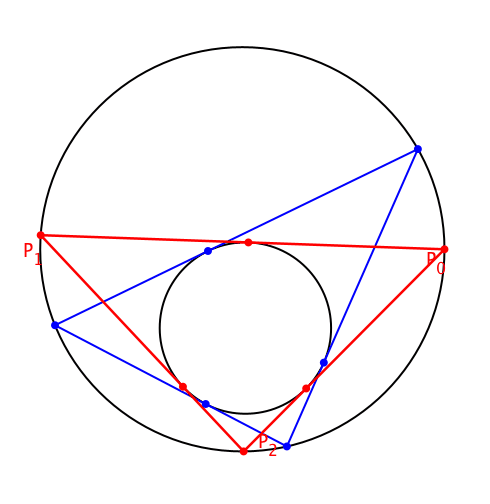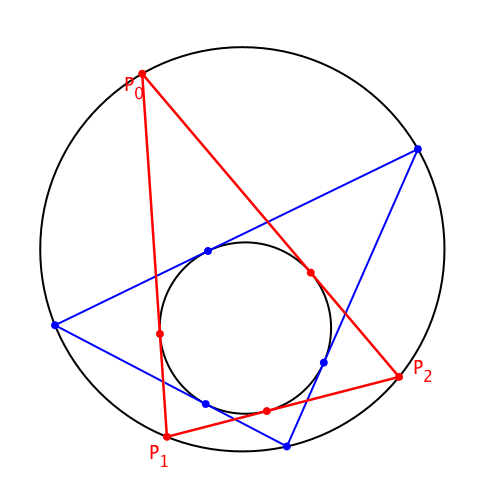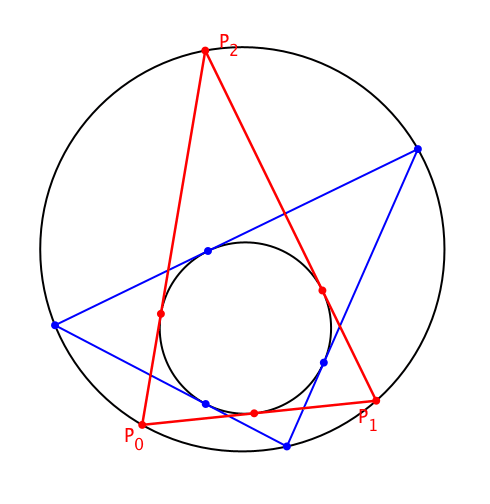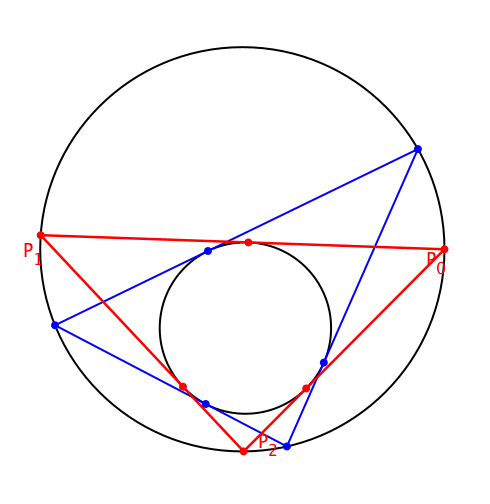
Abb. 6: Variation des Startpunktes

4 Beweis

Sonderfall eines Satzes von Poncelet.

Weblinks

Hans Walser: Schließungsfiguren

https://walser-h-m.ch/hans/Schliessungsfiguren/

Hans Walser: Inkreis und Umkreis

https://walser-h-m.ch/hans/Miniaturen/I/Inkreis_und_Umkreis/Inkreis_und_Umkreis.html