Hans Walser, [20240818]

Inkreis und Umkreis

1 Worum es geht

Zu einem Dreieck zeichnen wir den Umkreis und den Inkreis (Abb. 1):

Abb. 1: Dreieck mit Umkreis und Inkreis

Weiter zeichnen wir die drei Mittelsenkrechten der Strecken von den Dreiecksecken zum Inkreismittelpunkt (lila beziehungsweise magenta in Abb. 2).

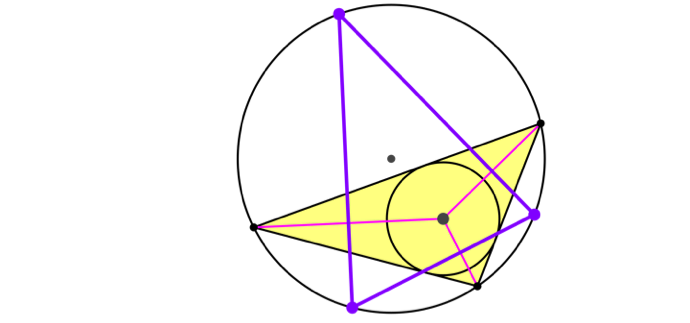
Abb. 2: Mittelsenkrechte

Die drei Mittelsenkrechten schneiden sich paarweise je in einem Punkt auf dem Umkreis.

2 Beweis

Wir arbeiten mit den Bezeichnungen der Abbildung 3.

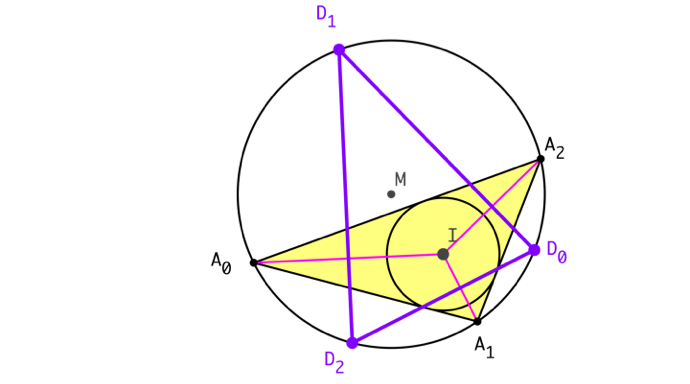
Abb. 3: Bezeichnungen

Zum Startdreieck A₀A₁A₂ zeichnen wir die inneren und äußeren Winkelhalbierenden (blau in Abb. 4).

Abb. 4: Winkelhalbierende

Die Punkte B₀, B₁ und B₂ sind die Mittelpunkte der Ankreise an das Startdreieck A₀A₁A₂. Im Winkelhalbierenden-Dreieck B₀B₁B₂ ist der Inkreismittelpunkt I des Startdreiecks der Höhenschnittpunkt. Daher ist der Umkreis u des Startdreiecks der Feuerbach-Kreis (Neunpunkte-Kreis) des Winkelhalbierenden-Dreiecks.

Wir zeichnen noch den Umkreis des Winkelhalbierenden-Dreiecks (blau in Abb. 5).

Abb. 5: Umkreis des Winkelhalbierenden-Dreiecks

Der Umkreis und der Feuerbachkreis eines Dreieckes sind perspektivähnlich. Das Perspektivitäts-Zentrum ist der Höhenschnittpunkt, der Perspektivitäts-Faktor ½. Die Abbildung 6 illustriert diesen Zusammenhang. Das Winkelhalbierenden-Dreieck B₀B₁B₂ wird durch eine zentrische Streckung mit dem Zentrum I und dem Faktor ½ auf das Dreieck D₀D₁D₂ abgebildet. Daraus ergibt sich der Sachverhalt mit den Mittelsenkrechten.

Abb. 6: Zentrische Streckung

Da die Punkte D₀, D₁ und D₂ zusätzlich auf den inneren Winkelhalbierenden des Startdreiecks A₀A₁A₂ liegen, halbieren sie die Bögen des Umkreises des Startdreiecks.

Es ist:

D₀ Halbierungspunkt des Bogens A₁A₂.

D₁ Halbierungspunkt des Bogens A₂A₀.

D₂ Halbierungspunkt des Bogens A₀A₁.

Beweis mit Peripheriewinkeleigenschaften.

Weblinks

Hans Walser: Inkreis und Umkreis

https://walser-h-m.ch/hans/Miniaturen/I/Inkreis_und_Umkreis/Inkreis_und_Umkreis.html