Hans Walser, [20140623]
Inkreise
Idee und Anregung: H. K. S., L.
1 Worum geht es?
Optimierungsfragen bei Inkreisen.
1.1 Beispiel 1
Den Sektoren eines regelm§igen n-Eckes werden Inkreise einbeschrieben (Abb. 1).

Abb. 1: Inkreise in Sektoren
Fr welches n ist der Flchenanteil der Inkreise gemessen an der Gesamtfigur am gr§ten?
1.2 Beispiel 2
Die Inkreise werden gem§ Abbildung 2 einbeschrieben.

Abb. 2: Malfatti
1.3 Beispiel 3
Kongruente Kreise werden einem gro§en Kreis gem§ Abbildung 3 einbeschrieben.

Abb. 3: Kreise im Kreis
2 Bearbeitung der Beispiele
2.1 Beispiel 1
Wir normieren den Umkreisradius des n-Eckes auf 1 und studieren ein gleichschenkliges Dreieck ABM mit der Schenkellnge 1 und dem Spitzenwinkel 2t (Abb. 4). In einem Sektordreieck eines regelm§igen n-Eckes ist t = ¹/n.
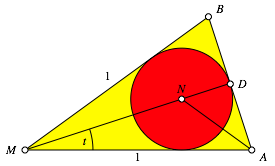
Abb. 4: Gleichschenkliges Dreieck
Der Flcheninhalt des Dreieckes ABM ist:
![]()
Wegen ![]() erhalten
wir:
erhalten
wir:
![]()
Somit ergibt sich fr die Inkreisflche:
![]()
Der Flchenanteil R(t) des Inkreises ist daher:
![]()
Im regelm§igen n-Eck ergibt sich der Flchenanteil S(n):
![]()
Die Tabelle 1 zeigt die numerischen Werte.
|
n |
S(n) |
|
3 |
0.3906748059 |
|
4 |
0.5390120850 |
|
5 |
0.5925741132 |
|
6 |
0.6045997883 |
|
7 |
0.5973173815 |
|
8 |
0.5809775641 |
|
9 |
0.5606209262 |
|
10 |
0.5388253167 |
|
11 |
0.5169325464 |
|
12 |
0.4956364887 |
|
13 |
0.4752808620 |
|
14 |
0.4560165897 |
|
15 |
0.4378877625 |
Tab 1: Numerische Werte fr Beispiel 1
Das Maximum ist beim regelm§igen Sechseck.
Die rote Kurve der Abbildung 5 stellt die Situation grafisch dar. Die blaue Kurve gibt die Ableitung.
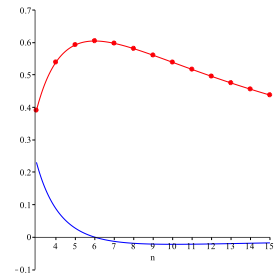
Abb. 5: Grafische Darstellung
2.2 Beispiel 2
Die Abbildung 6 zeigt einen Ausschnitt.
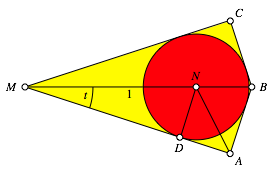
Abb. 6: Ausschnitt
Fr den Flcheninhalt des Drachenviereckes MABC erhalten wir:
![]()
Es ist ![]() und
und ![]() . Der Sinussatz liefert:
. Der Sinussatz liefert:
![]()
Somit hat der rote Inkreis den Flcheninhalt:
![]()
Der Inkreis hat den Flchenanteil:
![]()
Mit t = ¹/n ist:
![]()
Die Tabelle 2 zeigt die numerischen Werte:
|
n |
S(n) |
|
3 |
0.7290091126 |
|
4 |
0.7853981635 |
|
5 |
0.7656959550 |
|
6 |
0.7290091126 |
|
7 |
0.6892335410 |
|
8 |
0.6506451425 |
|
9 |
0.6146189620 |
|
10 |
0.5814960895 |
|
11 |
0.5512229720 |
|
12 |
0.5235987756 |
|
13 |
0.4983777586 |
|
14 |
0.4753125830 |
|
15 |
0.4541720216 |
Tab. 2: Beispiel 2
Das Maximum ist nun beim Quadrat.
Die rote Kurve der Abbildung 7 zeigt die Situation grafisch. Die blaue Kurve gibt die Ableitung.
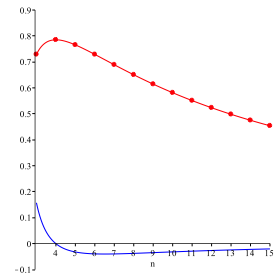
Abb. 7: Beispiel 2
2.3 Beispiel 3
Die Abbildung 8 ist an die Abbildung 4 angelehnt.
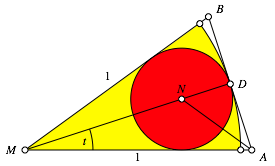
Abb. 8: Kreissektor
Der Flcheninhalt des Kreissektors ist:
![]()
Fr den Inkreis erhalten wir nach wie vor den Flcheninhalt:
![]()
Damit ergibt sich der Flchenanteil R(t):
![]()
Mit t = ¹/n ist:
![]()
Die Tabelle 3 zeigt die numerischen Werte. Dabei ist auch noch der Wert fr n = 2 eingefgt worden.
|
n |
S(n) |
|
2 |
0.5 |
|
3 |
0.6461709274 |
|
4 |
0.6862915016 |
|
5 |
0.6852102450 |
|
6 |
0.6666666667 |
|
7 |
0.6409393118 |
|
8 |
0.6128071030 |
|
9 |
0.5845582710 |
|
10 |
0.5572809001 |
|
11 |
0.5314616443 |
|
12 |
0.5072792491 |
|
13 |
0.4847543631 |
|
14 |
0.4638282272 |
|
15 |
0.4444047692 |
Tab. 3: Beispiel 3
Wir haben rationale Werte fr n = 2 und n = 6. Das Maximum ist bei n = 4.
Die rote Kurve der Abbildung 9 zeigt die Situation grafisch. Die blaue Kurve gibt die Ableitung.
Wenn wir fr n mit reellen Werten arbeiten, ist das Maximum zwischen 4 und 5.
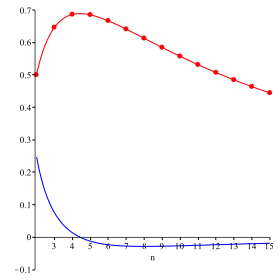
Abb. 9: Beispiel 3