Hans Walser, [20160630]

Inkreise von Bogendreiecken

1 Worum geht es?

Ein Bogendreieck hat Kreisbögen als Seiten.

Bei drei beliebigen Kreisen mit nicht leerem Durchschnitt der drei Kreisscheiben ergeben sich acht Bogendreiecke (Abb. 1).

Abb. 1: Acht Bogendreiecke

Das innerste Bogendreieck ist konvex, die drei anschließenden habe eine konkave Seite, die nächsten drei sogar je zwei konkave Seiten und die als Bogendreieck interpretierte Außenfläche hat drei konkave Seiten.

Die Abbildung 2 zeigt eine Situation mit leerem Durchschnitt der drei Kreisscheiben. Wo sind hier die Dreiecke?

Abb. 2: Leerer Durchschnitt

Im Folgenden beschränken wir uns auf die Situation der Abbildung 1.

2 Hyperbeln

Zu zwei Kreisen zeichnen wir die Hyperbel, welche die beiden Kreiszentren als Brennpunkte hat und durch einen Schnittpunkt der beiden Kreise verläuft (Abb. 3). Aus Symmetriegründen geht die Hyperbel auch durch den anderen Schnittpunkt. Die Punkte dieser Hyperbel haben von den beiden Kreislinien je denselben Abstand (magenta in Abb. 3). Dies ergibt sich unmittelbar aus der Abstandsdefinition der Hyperbel. Die Hyperbel hat also dieselbe Abstandseigenschaft wie die Winkelhalbierende in der Lineargeometrie. Tatsächlich halbiert sie auch den Schnittwinkel der beiden Kreise.

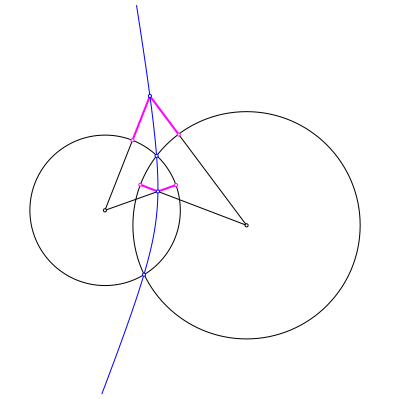
Abb. 3: Hyperbel

Wir zeichnen nun auch die Hyperbeln der beiden anderen Kreispaare (Abb. 4). Die nunmehr drei Hyperbeln haben einen gemeinsamen Schnittpunkt. Dies ergibt sich aus der Abstandseigenschaft. Der Schnittpunkt ist der Mittelpunkt des Inkreises des zentralen Bogendreieckes.

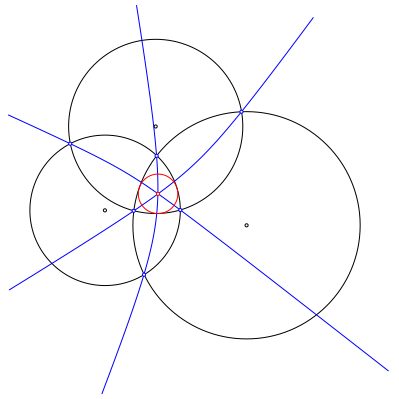
Abb. 4: Drei Hyperbeln und ein Inkreis

3 Die zweiten Hyperbeläste

Nun haben wir in der Schule gelernt, dass eine Hyperbel aus zwei „Ästen“ besteht. Die bildhafte Stimmigkeit dieser Bezeichnung hat sich mir nie erschließen wollen, aber die Eltern sind ja frei in der Namensgebung ihrer Kinder.

In der Abbildung 5 sind die zweiten Äste unserer Hyperbeln eingezeichnet.

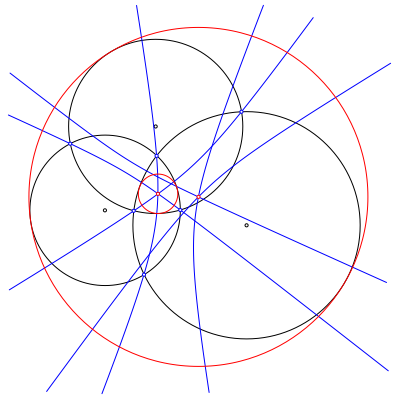
Abb. 5: Zweite Hyperbeläste

Diese zweiten Hyperbeläste haben auch einen gemeinsamen Schnittpunkt, und der ist der Mittelpunkt des Inkreises des Außendreiecks.

4 Ellipsen

In der Abbildung 6 wird die Konstruktion von zwei weiteren Inkreisen dargestellt. Die Mittelpunkte sind die gemeinsamen Schnittpunkte eines Hyperbelastes und zweier Ellipsen. Die Ellipsen haben wie die Hyperbeln zwei Kreiszentren als Brennpunkte und verlaufen durch die Schnittpunkte der zugehörigen Kreise.

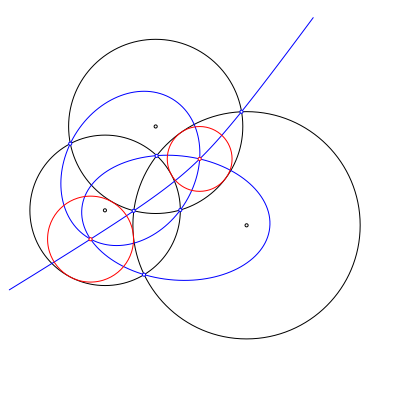
Abb. 6: Konstruktion mit einer Hyperbel und zwei Ellipsen

5 Übersicht

In der Abbildung 7 sind alle Kegelschnitte mit den Kreiszentren als Brennpunkten durch Schnittpunkte der Kreise dargestellt. An gemeinsamen Schnittpunkten sind entweder drei Hyperbeln oder eine Hyperbel und zwei Ellipsen beteiligt. Alle drei Ellipsen haben keinen gemeinsamen Schnittpunkt. Auch zwei Hyperbeln und eine Ellipse haben keinen gemeinsamen Schnittpunkt. Die Anzahl der an einem Schnittpunkt beteiligten Hyperbeln ist ungerade, die Anzahl der beteiligten Ellipsen gerade.

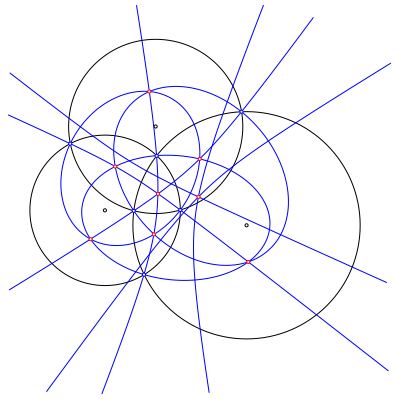
Abb. 7: Kegelschnitte

In der Abbildung 8 sind die acht Inkreise eingezeichnet.

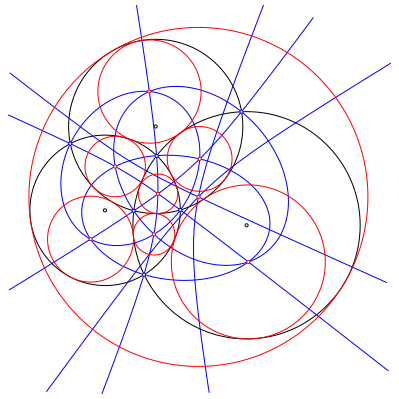
Abb. 8: Die acht Inkreise

Die Abbildung 9 enthält nur noch die Inkreise.

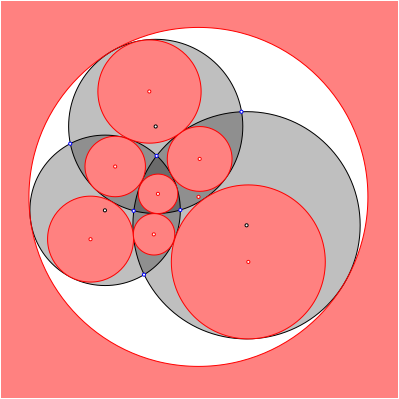
Abb. 9: Inkreise

6 Problem des Apollonius

Die Aufgabe, zu drei gegebenen Kreisen einen vierten Kreis zu finden, der die drei gegebenen Kreise berührt, geht auf Apollonius (Apollonius von Perge, ca. 262 BC – ca. 190 BC) zurück.

Das Problem ist mit Zirkel und Lineal lösbar, allerdings recht aufwändig.

Die hier vorgestellte einfache Lösung mit Kegelschnitten stammt von Adrian van Roomen (1561-1615).

7 Sonderfälle

Kreise mit Radius „unendlich“ sind Geraden. Die Abbildung 10 zeigt eine Situation mit zwei Kreisen (schwarz) und einer Geraden (schwarz).

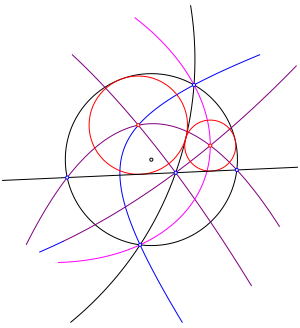
Abb. 10: Zwei Kreise und eine Gerade

Die blaue Kurve ist eine Hyperbel mit den Zentren der beiden Kreise als Brennpunkten, welche durch die Schnittpunkte der beiden Kreise verläuft.

Die lila Kurven sind Parabeln. Sie haben das Zentrum eines der beiden Kreise als Brennpunkt, die Symmetrieachse senkrecht zur Geraden und verlaufen durch die Schnittpunkte des Kreises mit der Geraden.

Die magenta Kurve ist eine Ellipse mit den Zentren der beiden Kreise als Brennpunkten, welche durch die Schnittpunkte der beiden Kreise verläuft.

Der Inkreis im Dreieck links hat sein Zentrum als Schnittpunkt der Hyperbel und zweier Parabeln.

Der Inkreis im Dreieck rechts hat sein Zentrum als Schnittpunkt zweier Parabeln und der Ellipse.

Die Abbildung 11 zeigt die volle Situation mit den acht Inkreisen.

Abb. 11: Acht Inkreise