Hans Walser, [20230607]

Inkreismittelpunktabschnitte

Anregung: Hans Humenberger, Wien

1 Worum es geht

Spielerei in der Dreiecksgeometrie.

2 Problemstellung

Von einem Dreieck kennen wir die drei Abschnitte von den Ecken bis zum Inkreismittelpunkt (grün in Abb. 1). Gesucht ist das Dreieck.

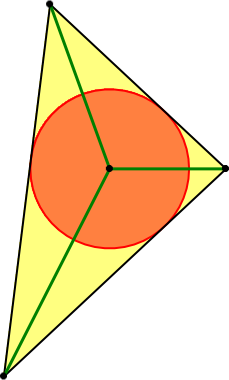
Abb. 1: Problemstellung

Die Abbildung 2 zeigt eine Schieberlösung. Der Schieber regelt den Radius r des roten Kreises.

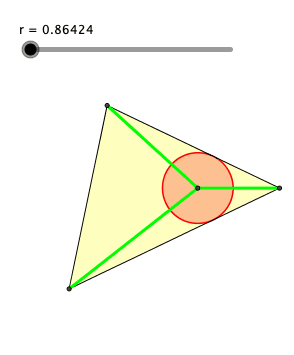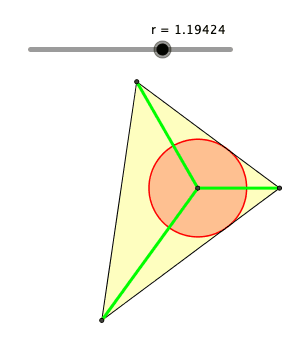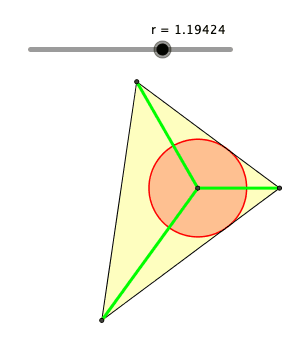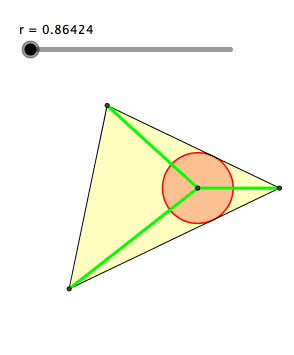
Abb. 2: Schieberlösung

Die grünen Abschnitte haben die Längen 2, 3 und 4. Der Inkreis ergibt sich für r ≈ 1.364244828.

3 Rechnerischer Zugang

Wir berechnen den Inkreisradius r.

Wir arbeiten mit den Bezeichnungen der Abbildung 3. AI, BI, CI sind die drei gegebenen Abschnitte.

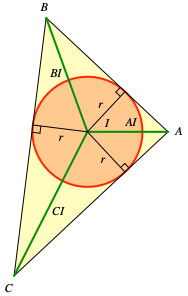
Abb. 3: Bezeichnungen

Es ist:

arccos(r/AI) + arccos(r/BI) + arccos(r/CI) = π

Diese Gleichung lösen wir mit CAS nach r auf.

Für die Abschnitte mit den Längen 2, 3 und 4 ergibt sich r ≈ 1.364244828. Es treten kubische Wurzeln auf. Lösungsweg daher nicht mit Zirkel und Lineal nachvollziehbar.

Eine Variante ist die Gleichung:

arcsin(r/AI) + arcsin(r/BI) + arcsin(r/CI) = π/2

Sie liefert dieselbe Lösung.

Weblinks

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte4/Hoehenabschnitte4.html