Hans Walser, [20100615c]

Inparabeln

Anregung: [Göbels 2010]

1 Worum geht es?

Einem Dreieck werden Parabeln einbeschrieben. Dies geschieht am elegantesten unter Verwendung von Bézier-Kurven. Es ergeben sich aber mehrere andere Möglichkeiten, diese Parabeln zu bestimmen.

Die Brennpunkte und Leitlinien der drei Parabeln führen zu zwei Schnittpunkten und einem Fünfpunktekreis im Dreieck.

2 Und hier die Definition

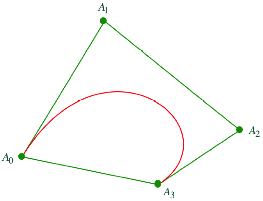
Unter der Inparabel eines Dreieckes verstehen wir die Bézier-Kurve zweiten Grades mit den Stützpunkten (Indizes modulo 3).

Die Abbildung zeigt links die Inparabel , rechts alle drei Inparabeln.

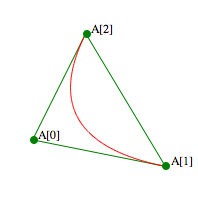
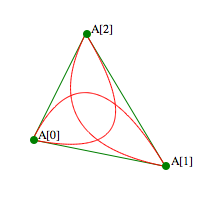
Inparabeln

3 Eigenschaften der Bézier-Kurven zweiten Grades

Bézier-Kurven zweiten Grades sind Parabeln (zweiten Grades) im Sinne der Kegelschnitte. Der Name Inparabel ist also in unserem Kontext gerechtfertigt.

Vorsicht: In der grafischen Praxis werden in der Regel Bézier-Kurven dritten Grades verwendet. Diese benötigen vier Stützpunkte und sind in der Regel keine Parabeln dritten Grades. Wir können die vier Stützpunkte sogar nichtplanar wählen, dann ist auch die zugehörige Bézier-Kurve nicht eben.

Unsere Bézier-Kurven zweiten Grades können als Parameterkurven dargestellt werden:

Die Parabel berührt die Seite im Punkt , die Seite im Punkt und die Mittelparallele im Schnittpunkt mit der Schwerlinie . Dies ergibt sich aus dem Casteljau-Algorithmus der Bézier-Kurven. Entsprechendes gilt für die Inparabeln und .

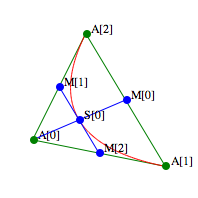
Berührungen

Damit haben wir schon 6 Bedingungen, welche die Parabel als Kegelschnitt festlegen. Tatsächlich ist ein Kegelschnitt durch 5 Bedingungen festgelegt, unsere 6 Bedingungen sind also redundant.

4 Verallgemeinerung

Das Konzept der Inparabeln lässt sich auf beliebige, auch nicht konvexe, Polygone verallgemeinern. Als Beispiele ein Viereck und ein regelmäßiges Pentagramm.

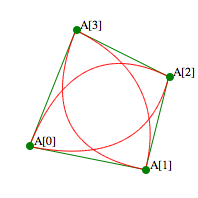
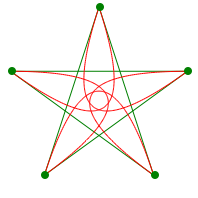
Inparabeln in Viereck und Pentagramm

5 Fadengrafik. Enveloppen

Aus dem Casteljau-Algorithmus der Bézier-Kurven ergibt sich die Darstellung der Inparabeln als Enveloppe oder „Fadengrafik“. Für die Ansatzpunkt der Fäden werden die Dreiecksseiten regelmäßig in je gleich viele Teile unterteilt. Als Beispiele und Bastelanleitungen das gleichseitige Dreieck und das Quadrat.

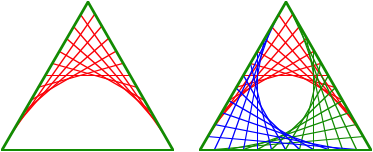
Fadengrafik im Dreieck

Fadengrafik im Quadrat

6 Achse und Brennpunkt der „schrägen“ Parabeln

6.1 Achsenrichtung

Wir kehren zunächst das Problem um und zeichnen zur Schulparabel ein passendes Dreieck. Dies geschieht durch zwei Tangenten mit Berührpunkten und . Die beiden Tangenten schneiden sich in .

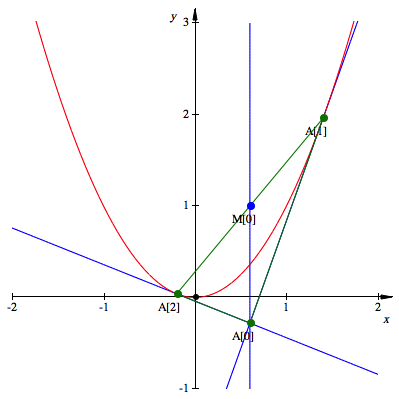
Das Dreieck wird passend gemacht

Nun ist es eine alt gediente Schulaufgabe, zu zeigen, dass die x-Koordinate von der Mittelwert der x-Koordinaten von und ist. Die Schwerlinie des Dreieckes ist also parallel zur Parabelachse. Da alle Parabeln ähnlich sind, folgt, dass die Symmetrieachse der Inparabel jeweils parallel zur entsprechenden Schwerlinie ist.

6.2 Brennpunkt und ein Schnittpunkt

Den Brennpunkt der Inparabel finden wir nun über die Reflexionseigenschaft der Parabel. Wir legen Parallelen zu durch die Punkte und und spiegeln diese Parallelen an beziehungsweise an . Die beiden reflektierten Geraden schneiden sich im Brennpunkt .

Zwei Geraden in allgemeiner Lage schneiden sich in einem Punkt. Wenn dies drei Geraden tun, ist das bemerkenswert wie zum Beispiel bei den drei Höhen im Dreieck (vgl. [Walser 2004]). Einen solchen bemerkenswerten Schnittpunkt finden wir im Parallelogrammraster. Wir zeichnen einige Diagonalen ein und spiegeln gemäß Figur. Die Spiegelbilder der drei Diagonalen schneiden fokussieren auf denselben Punkt. Der Beweistipp liegt in der Formulierung „fokussieren“.

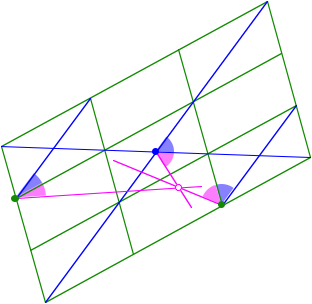
Schnittpunkt mit gespiegelten Diagonalen

6.3 Symmetrieachse

Die Parallele zu durch den Brennpunkt ist nun die Symmetrieachse. Wir können nun die Punkte und an dieser Symmetrieachse spiegeln und erhalten und . Zusammen mit dem Punkt haben wir nun insgesamt fünf Punkte auf der Parabel. Damit ist der Kegelschnitt definiert und kann entsprechend zum Beispiel mit DGS gezeichnet werden.

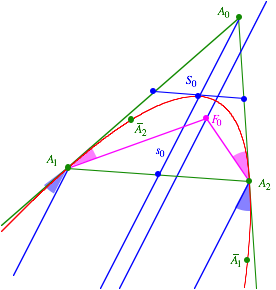
Konstruktion mit DGS

7 Was es sonst noch gibt

7.1 Der Umkreis kommt ins Spiel

Der Brennpunkt , die Punkte und sowie der Umkreismittelpunkt U des Dreieckes liegen ihrerseits auf einem Kreis. Dies kann mit Winkelüberlegungen als Folge der Reflexionskonstruktion des Brennpunktes eingesehen werden.

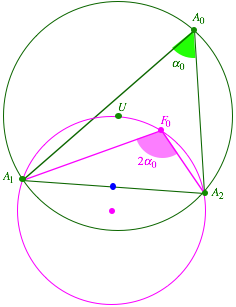
Punkte auf einem Kreis

7.2 Die drei Brennpunkte und noch ein Schnittpunkt

Die Brennpunkte der drei Inparabeln sowie der Umkreismittelpunkt liegen auf einem Kreis. Verifikation durch DGS, Beweis fehlt.

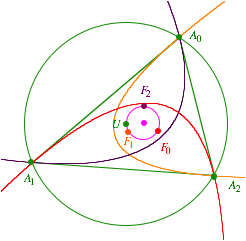
Noch ein Kreis

Weiter ist es so, dass die drei Geraden , und sich in einem gemeinsamen Punkt F schneiden. Dieser Punkt liegt ebenfalls auf dem Kreis durch die drei Brennpunkte, und zwar diametral zum Umkreismittelpunkt U. Verifikation durch DGS, ohne Beweis. Wir haben also einen Fünfpunktekreis. Für einen weitere Fünfpunktekreise im Dreieck siehe [Walser 2009].

Ein Schnittpunkt

7.3 Die drei Leitlinien und noch ein weiterer Schnittpunkt

Die Leitlinien der drei Inparabeln bilden das Leitliniendreieck gemäß Figur. Die drei Geraden , und schneiden sich in einem gemeinsamen Punkt L. Verifikation DGS, ohne Beweis.

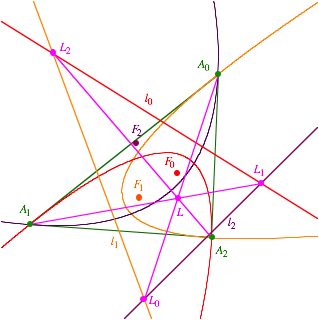
Leitliniendreieck und kopunktale Geraden

7.4 Umparabeln

Wir spiegeln den Seitenmittelpunkt an der Dreiecksecke und erhalten so den Punkt . Die Inparabel des Dreieckes ist dann die Umparabel des Dreieckes . Sie verläuft durch alle drei Ecken.

Die Figur zeigt die drei Umparabeln.

Umparabeln

8 Didaktisches

8.1 Der Zeitgeist

Zur Zeit ist es wieder Mode geworden, im Schulunterricht zu „modellieren“.

Zur Modellierung von Kurven werden die Funktionsgrafen von Polynomfunktionen strapaziert, obwohl Funktionsgrafen das denkbar schlechteste Werkzeug zur Kurvenmodellierung sind. Kein Kreis lässt sich so darstellen, ja nicht einmal eine senkrechte Gerade. Besser geeignet wären parametrisierte Darstellungen von Kurven. Ein Sonderfall dazu sind Bézier-Kurven (meist dritten Grades, vgl. Beispiel), welche in jeder Grafiksoftware implementiert sind.

Bézier-Kurve dritten Grades

Das Problem liegt im Funktionsbegriff, indem es zu einem x nicht zwei verschiedene y geben darf (Schülersprache). Es muss also eine Richtung geben, in der die Kurve nur einmal geschnitten wird.

Ein weiteres Problem ist, dass die physikalischen und statischen Gegebenheit es oft nicht zulassen, im Schulunterricht eine korrekte Lösung zu erarbeiten. Daher wird dann nur noch der äußere Schein modelliert. Ich habe tatsächlich schon Arbeitsblätter gesehen, in denen eine zwischen zwei Aufhängepunkten durchhängende Kette durch eine quadratische Parabel modelliert werden sollte. Da das echte Problem, eine Variationsaufgabe, zu schwierig ist, greift man zur Näherungslösung. Allerdings könnte ebenso gut der Kreis als Näherungslösung verwendet werden.

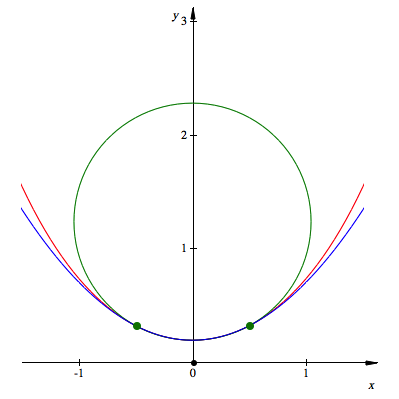
Die durchhängende Kette mit Näherungslösungen

8.2 Bézier-Kurven im Unterricht

Da Bézier-Kurven erst in der Mitte des letzten Jahrhunderts entwickelt wurden, haben sie noch kaum Eingang in den Schulunterricht gefunden. Dabei wären sie eine ideale Möglichkeit, Parameterdarstellungen allgemein und insbesondere die Parameterdarstellung der Geraden sowie die binomische Formel zu vertiefen.

Ein sehr schönes Arbeitsheft dazu ist [Dzung Wong 2003].

Literatur

[Dzung Wong 2003] Dzung Wong, Baoswan: Bézierkurven gezeichnet und berechnet. Zürich: Orell Füssli 2003. ISBN 3-280-04021-3

[Göbels 2010] Göbels, Wolfgang: Einbeschriebene und umhüllende Parabeln. MNU Der mathematische und naturwissenschaftliche Unterricht 63/3 (15. 4. 2010), S. 152-154, ISSN 0025-5866, © Verlag Klaus Seeberger, Neuss.

[Walser 2004] Walser, Hans: 99 Schnittpunkte. Beispiele – Bilder – Beweise. Edition am Gutenbergplatz, Leipzig 2004. ISBN 3-937219-10-2

[Walser 2009] Walser, Hans: Fünfpunktekreise. MNU Der mathematische und naturwissenschaftliche Unterricht 62/3 (15. 4. 2009), S. 146, ISSN 0025-5866 .