Hans Walser, [20191223]
Invariante Quadratsumme
1 Worum geht es?
Beweis des Satzes des Pythagoras mit Mitteln der Infinitesimalrechnung.
2 Invarianz im Gro§en
Wenn wir die Ecke mit dem rechten Winkel auf dem Thaleskreis bewegen, bleibt die Summe der Quadrate der Katheten invariant (Abb. 1).
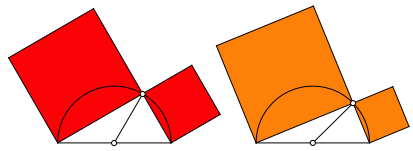
Abb. 1: Rot = orange
Wir versuchen, dies ohne Rźckgriff auf das Hypotenusenquadrat zu beweisen.
3 Invarianz im Kleinen
Wir studieren, was bei einer infinitesimal kleinen Bewegung der Ecke mit dem rechten Winkel geschieht. Die Abbildung 2 zeigt eine kleine Bewegung, welche wir als infinitesimal klein uns denken.

Abb. 2: Kleine Bewegung
Das hellblau eingezeichnete Dreieck ist praktisch Šhnlich – und bei einer infinitesimal kleinen Bewegung źberhaupt Šhnlich – zum ursprźnglichen rechtwinkligen Dreieck.
Die Katheten des blauen Dreiecks geben die VerŠnderungen der gro§en Katheten a und b, und zwar ist:
![]() (1)
(1)
Das Minuszeichen kommt daher, dass sich a verkleinert, aber b vergrš§ert.
Aus (1) ergibt sich:
![]() (2)
(2)
Wir studieren nun die €nderung der Summe der Quadrate der beiden Katheten.
![]() (3)
(3)
Die Summe der Quadrate der beiden Katheten bleibt also źberall lokal und damit global invariant. Dies war zu zeigen.
Die
Gleichheit mit dem Hypotenusenquadrat folgt aus dem Grenzfall ![]() .
.
4 Randbemerkung: Andersherum gedreht
Es ist in der Schule źblich, die Ecke mit dem rechten Winkel auf dem Thaleskreis zu bewegen (Abb. 1, 2, 5).
Ebenso gut kšnnten wir diese Ecke festlassen und die Hypotenuse im Thaleskreis drehen (Abb. 3, 4, 6, 7).
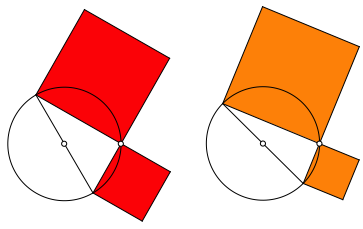
Abb. 3: Rot = orange
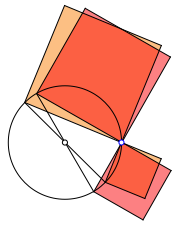
Abb. 4: Rot = orange. †berlagerung
Die Animation 1 zeigt den Sachverhalt.
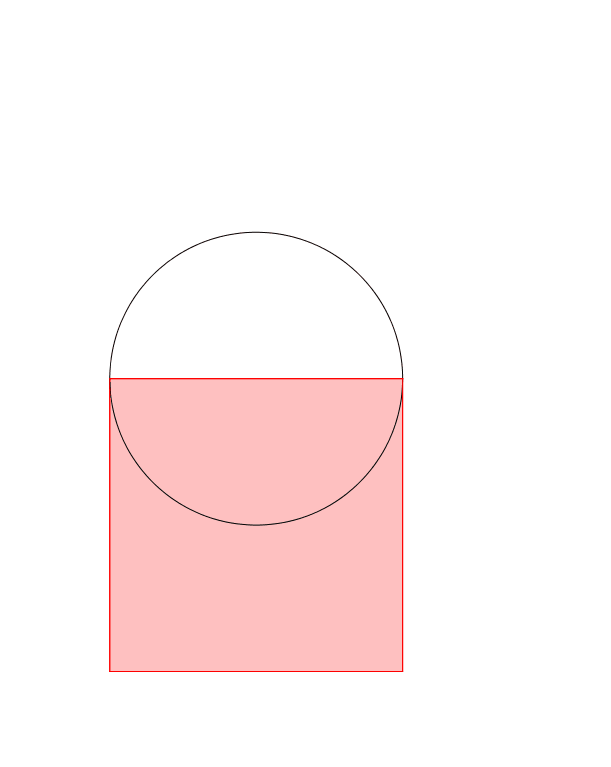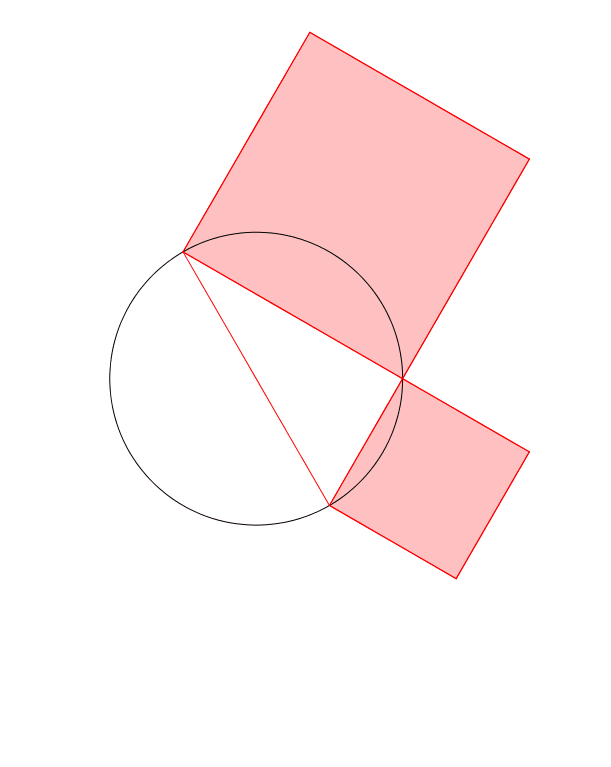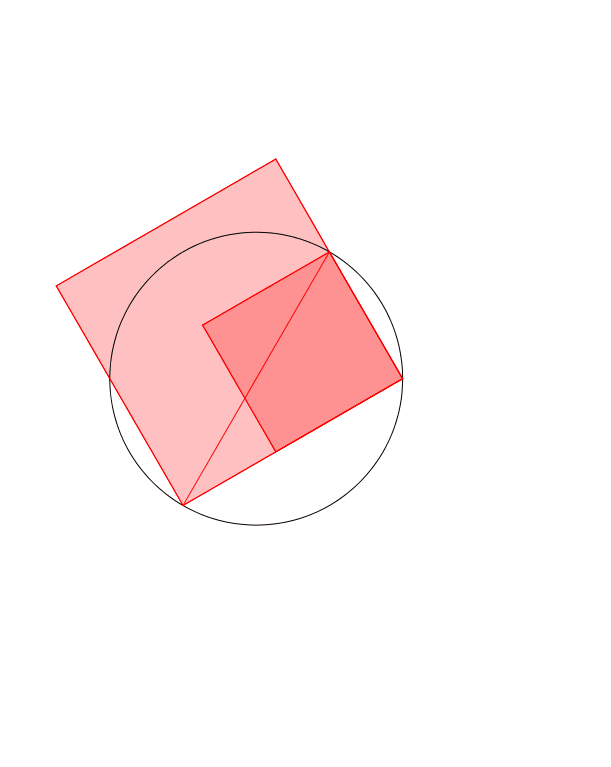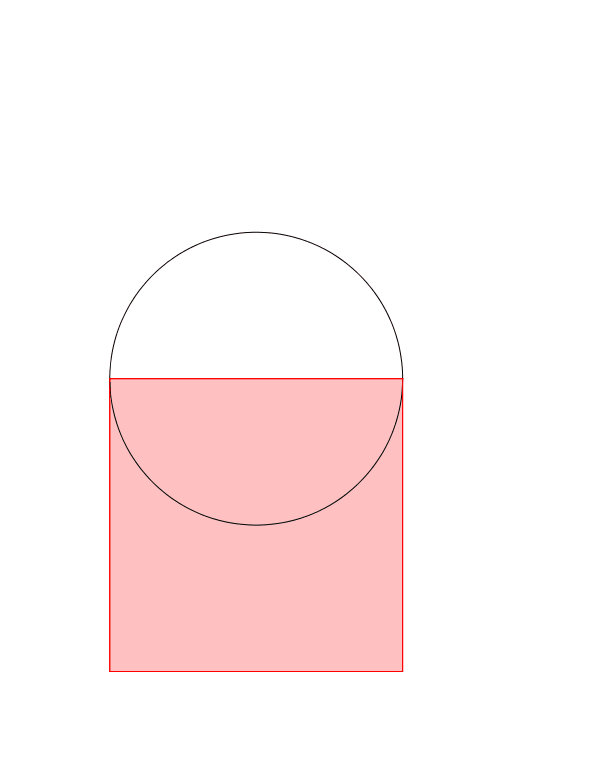
Animation 1: Drehen der Hypotenuse
5 Zerlegungsbeweise
5.1 Feste Hypotenuse
Die
Abbildung 5 zeigt einen Zerlegungsbeweis fźr die Invarianz der Summe der Kathetenquadrate.
Die Hypotenuse ist fest, die Ecke beim rechten Winkel variiert auf dem
Thaleskreis. Die Teile lassen sich translatorisch ineinander źberfźhren.
Hintergrund ist der Zerlegungsbeweis von Perigal. Es braucht ![]() Teile.
Teile.
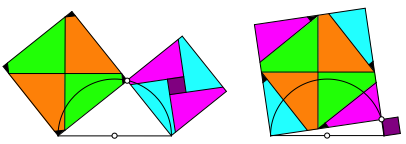
Abb. 5: Zerlegungsbeweis
5.2 Fester Eckpunkt beim rechten Winkel
Die Abbildung 6 zeigt einen Zerlegungsbeweis mit festem Eckpunkt beim rechten Winkel. Es wird die Hypotenuse gedreht. Es braucht acht Teile.
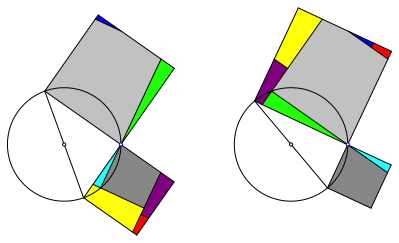
Abb. 6: Drehen der Hypotenuse
Die Teile kšnnen translatorisch oder durch Drehungen um Vielfache von 90ˇ ineinander źbergefźhrt werden. Die grauen Teile bleiben ortsfest.
Die Abbildung 7 zeigt die †berlagerung der beiden Figuren der Abbildung 6.
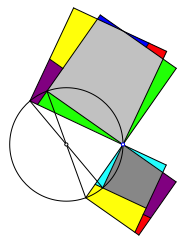
Abb. 7: †berlagerung
Websites
Hans Walser: Invarianzbeweis fźr den Satz des Pythagoras
www.walser-h-m.ch/hans/Miniaturen/I/Invarianzbeweis_Pythagoras/Invarianzbeweis_Pythagoras.htm