Hans Walser, [20220520]
Invarianter Schwerpunkt
Idee und Anregung: Thomas Jahre, Aufgabe 60-713
1 Konstruktionsvorgang
Wir beginnen mit einem beliebigen Dreieck ABC (Abb. 1).
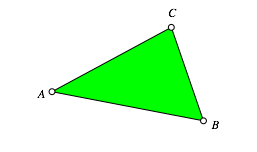
Abb. 1: Startdreieck
Den drei Seiten setzen wir gleichsinnig Šhnliche Dreiecke an (Abb. 2).
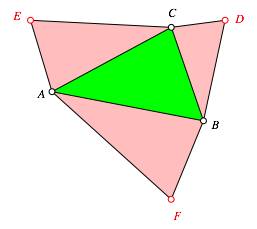
Abb. 2: €hnliche Dreiecke ansetzen
Das Ansetzen geschieht so, dass wir an den Au§enecken D, E und F gleiche Winkel haben.
2 Schwerpunkte
Es sei S der Schwerpunkt (Eckenschwerpunkt) des Dreieckes ABC (Abb. 3).
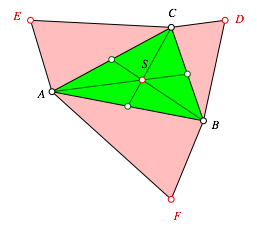
Abb. 3: Eckenschwerpunkt
Weiter sei T der Schwerpunkt der drei Punkte D, E und F.
Es zeigt sich nun, dass T = S (Abb. 4).
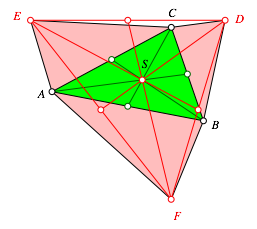
Abb. 4: Invarianter Schwerpunkt
3 Beweis
Wir arbeiten in der Ebene der komplexen Zahlen.
ZunŠchst ist:
![]()
Weiter ist wegen der €hnlichkeit:
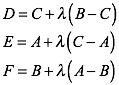
Dabei ist λ ebenfalls eine komplexe Zahl.
Daraus berechnet sich:
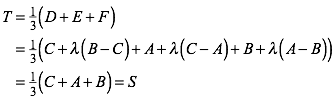
Dies war zu zeigen.
4 Folgerungen
(1) Der Schwerpunkt S ist nun auch der Schwerpunkt aller sechs Punkte A, B, C, D, E, F.
(2) Die Šhnlichen roten Dreiecke kšnnen durch beliebige Šhnliche Polygone ersetzt werden. Die Abbildung 5 zeigt ein Beispiel mit Šhnlichen Vierecken.
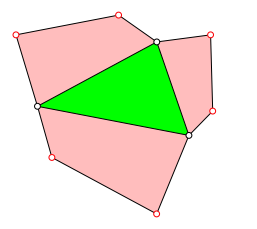
Abb. 5: €hnliche Vierecke
Der Schwerpunkt der insgesamt neun Punkte ist derselbe wie der Schwerpunkt der drei Eckpunkte des grźnen Dreieckes.
(3) Ein Sonderfall obiger Situation ist die Figur des Pythagoras mit einem rechtwinkligen Dreieck und drei angesetzten Quadraten.
(4) Das grźne Dreieck kann durch ein beliebiges Polygon ersetzt werden. Beweis analog.
Weblink
Thomas Jahre: Aufgabe der Woche