Hans Walser, [20180321]
Invariantes Produkt
Anregung: K. H., Gš.
1 Worum geht es?
Ein elementargeometrisches Beispiel eines invarianten Produktes fŸhrt zu einer Konstruktion der Bernoullischen Lemniskate.
2 Einheitskreis mit Gigampfi
Wir passen einen Einheitskreis in einen Streifen ein (Abb. 1).
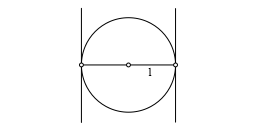
Abb. 1: Einheitskreis im Streifen
Eine weitere Tangente an den Einheitskreis (Gigampfi, Wippe) fŸhrt zu den Tangentenabschnitten p und q (Abb. 2).
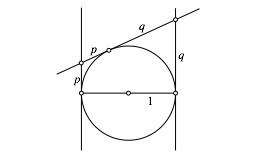
Abb. 2: Gigampfi
3 Invariantes Produkt
In der Situation der Abbildung 2 gilt:
(1)
4 Beweise
4.1 Pythagoras
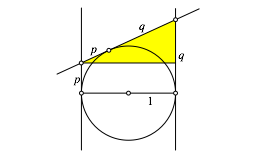
Abb. 3: Pythagoras
Im markierten rechtwinkligen Dreieck (Abb. 3) gilt nach dem Satz des Pythagoras:
(2)
Durch Umformen ergibt sich (1).
4.2 Hšhensatz
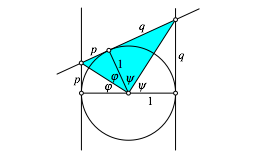
Abb. 4: Hšhensatz
Das markierte rechtwinklige Dreieck (Abb. 4) hat die Hypotenusenhšhe 1 und die Hypotenusenabschnitte p und q. Aus dem Hšhensatz ergibt sich (1).
4.3 Trigonometrie
Die
Winkel 
und 
ergŠnzen
sich auf 90¡. Es ist daher:
(3)
Daraus ergibt sich (1).
5 Lemniskate
Die in der Abbildung 5 blau eingezeichneten Kreise schneiden sich in der rot eingezeichneten Bernoullischen Lemniskate.
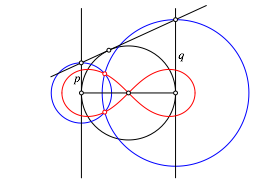
Abb. 5: Lemniskate
Reelle Schnittpunkte gibt es allerdings nur, wenn sich er BerŸhrungspunkt der Gigampfi im rot markierten Bereich des Einheitskreises (Abb. 6) befindet.
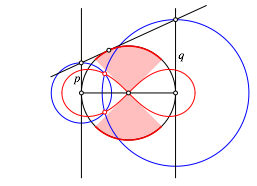
Abb. 6: Bereich fŸr reelle Lemniskatenpunkte