Hans Walser, [20200110]
Invarianzbeweis fźr den Satz des Pythagoras
1 Worum geht es?
Invarianzbeweis mit einer Zerlegung
2 Klassische Darstellung
Der Satz des Pythagoras wird in der Regel mit drei Quadraten illustriert (Abb. 1).
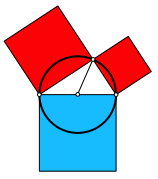
Abb. 1: Rot = blau
Bei einer Verschiebung der Ecke mit dem rechten Winkel auf dem Thaleskreis bleibt das blaue Hypotenusenquadrat fest. Daher ist auch die FlŠchensumme der beiden roten Kathetenquadrate invariant.
3 Invarianz
Die Frage ist, ob diese Invarianz auch ohne Bezugnahme auf das Hypotenusenquadrat gezeigt werden kann (Abb. 2).
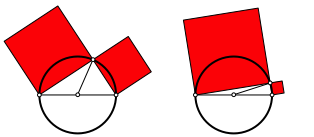
Abb. 2: Invariante FlŠchensumme
4 Zerlegungsbeweis
Die Abbildung 3 zeigt eine gemeinsame Zerlegung.
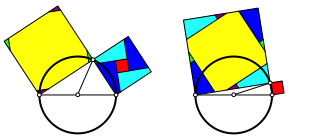
Abb. 3: Zerlegungsbeweis
Websites
Hans Walser: Invarianzbeweis fźr den Satz des Pythagoras
www.walser-h-m.ch/hans/Miniaturen/I/Invarianzbeweis_Pythagoras/Invarianzbeweis_Pythagoras.htm
Hans Walser: Invarianzbeweis fźr den Satz des Pythagoras
www.walser-h-m.ch/hans/Miniaturen/I/Invarianzbeweis_Pythagoras2/Invarianzbeweis_Pythagoras2.htm