Hans Walser, [20120607]

Irrationalität und DIN

Mit Hilfe von DIN-Papieren kann die Irrationalität von nachgewiesen werden. Der beweis läuft wie üblich indirekt.

Wir nehmen an. Dann kann als Bruch teilerfremder natürlicher Zahlen a und b geschrieben werden:

Es ist weiter , aber .

Da ein DIN A5-Papier das Seitenverhältnis hat, gibt es eine geeignete Maßeinheit, so dass das A5-Papier an der langen Seite a Einheiten misst und an der kurzen Seite b (Abb. 1).

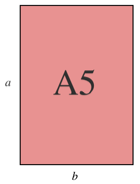
Abb. 1: Ganzzahlige Maße im A5-Papier

Wenn wir zwei solcher A5-Papiere aneinanderfügen, entsteht ein A4-Rechteck mit der langen Seite 2b und der kurzen Seite a (Abb. 2).

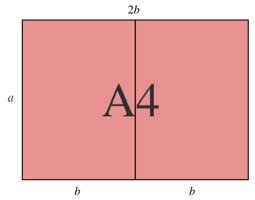
Abb. 2: A4-Rechteck

Nun legen wir die beiden A5-Papiere im Querformat auf das A4-Rechteck (ebenfalls im Querformat) gemäß Abb. 3.

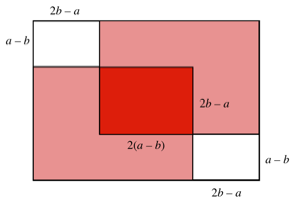
Abb. 3: Umgelegte A5-Papiere

Es entstehen neue Rechtecke, in der Mitte ein Überlappungsrechteck und an zwei diametralen Ecken je ein Lochrechteck. In der Abbildung 3 sind die Maße dieser neuen Rechtecke angegeben.

Mit Strahlensatzüberlegungen folgt, dass alle Rechtecke ähnlich sind, also das Seitenverhältnis haben. Somit ergibt sich aus dem Überlappungsrechteck:

Wenn wir der Abbildung 3 trauen dürfen, ist das ein Bruch mit kleinerem Zähler und Nenner als . Dies steht im Widerspruch dazu, dass als optimal gekürzt angenommen wurde. Wir müssen aber wirklich noch zeigen, dass zum Beispiel . Das geht so: Oben hatten wir: . Daraus folgt:

Damit ist der Widerspruch zur Annahme nachgewiesen. Es ist . Für andere Irrationalitätsbeweise von siehe [Miller/Montague 2012].

Aufgabe: In ein A4-Rechteck legen wir zwei A5-Rechtecke gemäß Abbildung 4.

Es entstehen ein Überlappungsrechteck und zwei Lochrechtecke.

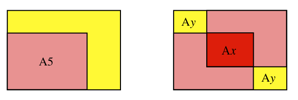
Abb. 4: Zwei A5-Rechtecke im A4-Rechteck

Welchen A-Code haben das Überlappungsrechteck und die Lochrechtecke?

Bearbeitung

Wir nehmen für das A4-Rechteck die Länge und die Breite 1 an. Der Flächeninhalt des A4-Rechteckes ist also . Für die neuen Rechtecke ergeben sich die Maßverhältnisse der Abbildung 5.

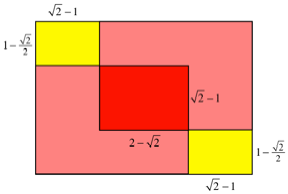
Abb. 5: Maßverhältnisse

Für das Überlappungsrechteck erhalten wir den Flächeninhalt:

Das A4-Recheck hat den Flächeninhalt . Nun gilt folgende Flächenverhältnisgleichung:

Dies ist eine Exponentialgleichung mit der Lösung:

Das Überlappungsrechteck rangiert zwischen A6 und A7.

Für ein Lochrechteck erhalten wir den Flächeninhalt:

Somit gilt:

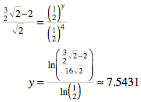
Diese letzte Rechnung hätten wir uns sparen können: Da die beiden A5-Rechtecke zusammen flächenmäßig gleich groß sind, ist das Überlappungsrechteck flächenmäßig doppelt so groß wie ein Lochrechteck. Diese haben somit einen um 1 größeren A-Code.

Literatur

[Miller/Montague 2012] Miller, Steven J. and Montague David: Picturing Irrationality. Mathematics Magazine. 85 (2012), p. 110-114.