Hans Walser, [20180301]

Isogonale Vielecke

Anregung: V. A. K., D.

1     Worum geht es

Die Abbildung 1 zeigt ein isogonales Vieleck. Es hat sechs gleiche Winkel. Weiter hat es dieselben Symmetrien wie das regelmŠ§ige Dreieck.

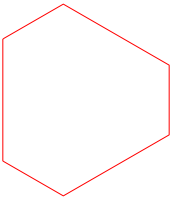
Abb. 1: Isogonales Vieleck

Dieses Vieleck soll nun in Polarkoordinaten  dargestellt werden. Dabei, und das ist das Neckische, soll die Funktion  ohne Fallunterscheidungen formuliert werden.

2     Lšsung

Die Funktion

 

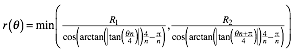                                       (1)

 

 

 

lšst das Problem. Herleitung in Anlehnung an [1] .

Die vorkommenden Parameter haben folgende geometrische Bedeutung: n ist die halbe Eckenzahl des isogonalen Vieleckes. R1 ist der Abstand der langen Seiten vom Ursprung, R2 der Abstand der kurzen Seiten vom Ursprung.

Im Beispiel der Abbildung 1 ist n = 3, R1 =1  und R2 = 1.2.

Fźr R2 = R1 erhalten wir das regelmŠ§ig 2n-Eck.

3     Weitere Beispiele

Die Abbildung 2 zeigt den Fall fźr n = 4, R1 =1 und R2 = 1.2. Wir haben die Symmetrien des Quadrates.

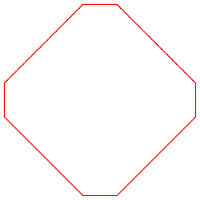
Abb. 2: Isogonales Achteck

Die Formel (1) funktioniert auch fźr rationale n. Die Abbildung 3 zeigt die Situation fźr n = 4.5, R1 =1 und R2 = 1.2.

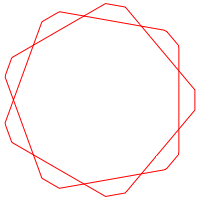
Abb. 3: Isogonales Achtzehneck

Wir mźssen fźr den Polarwinkel  zwei UmlŠufe vorsehen: . Der Parameter n ist daher nur noch ein Viertel der Eckenzahl.

Wir haben die Symmetrien des regelmŠ§igen Neuneckes.

4     Diskussion der Lšsung

Die Formel (1) enthŠlt auf den ersten Blick keine Fallunterscheidung. Auf den zweiten Blick sehen wir, dass die Betragsfunktion und die Minimumfunktion vorkommen. Beides sind von der Definition her Funktionen mit einer dichotomen Fallunterscheidung. Allerdings kšnnen wir dieses Problem beheben.

4.1    Betragsfunktion

GemŠ§ źblicher Definition ist:

 

                                                                                                     (2)

 

 

 

Wir kšnnen diese Fallunterscheidung umgehen mit:

 

                                                                                                                         (3)

 

 

4.2    Minimumfunktion

GemŠ§ źblicher Definition ist:

 

                                                                                         (4)

 

 

 

Wir kšnnen diese Fallunterscheidung umgehen mit:

 

                                                                                           (5)

 

 

Die in (5) erscheinende Betragsfunktion kšnnen wir durch (3) substituieren.

5     Programm

Die Abbildung 4 zeigt das fźr die Abbildung 1 verwendete Programm (Maple):

 

restart: with(plots): with(plottools):

 

n := 3: # halbe Eckenzahl

 

R1 := 1: # erster Radius

 

R2 := 1.2: # zweiter Radius

 

r := t -> min(R1/cos(arctan(abs(tan(t*n/4)))*4/n-Pi/n), R2/cos(arctan(abs(tan((t*n+Pi)/4)))*4/n-Pi/n)):

 

Figur := plot(r(t), t=0..2*Pi, thickness=1, color=red, coords = polar):

 

display([Figur], scaling = constrained, axes = none);

Abb. 4: Programm

 

Website

[1] Hans Walser: Polardarstellung eines regelmŠ§igen Vielecks (abgerufen 01.03.2018):

www.walser-h-m.ch/hans/Miniaturen/P/Polardarst_Vieleck/Polardarst_Vieleck.htm