Hans Walser, [20150809]
Isoperimetrische Vielecke mit gegebenen Seitenlngen
Anregung: Chr. K., B.
1 Worum geht es
Unter
allen n-Ecken mit gegebenen
Seitenlngen ![]() hat
dasjenige den gr§ten Flcheninhalt, dessen Ecken
hat
dasjenige den gr§ten Flcheninhalt, dessen Ecken ![]() auf einem
Kreis liegen (Sehnen-n-Eck).
auf einem
Kreis liegen (Sehnen-n-Eck).
Es sind also, im Unterschied zu den blichen isoperimetrischen Problemstellungen, nicht nur der globale Umfang, sondern auch die einzelnen Seitenlngen gegeben.
Der Beweis geht in zwei Schritten. Zunchst wird der Sachverhalt fr das Viereck bewiesen, und anschlie§end verallgemeinert.
2 Viereck
Zu zeigen
ist: Unter allen Vierecken mit gegebenen Seiten ![]() hat das Sehnenviereck
den gr§ten Flcheninhalt.
hat das Sehnenviereck
den gr§ten Flcheninhalt.
Fr den
Beweis zerlegen wir das Viereck (Abb. 1) mit der Diagonalen ![]() in zwei
Dreiecke
in zwei
Dreiecke ![]() und
und ![]() .
.
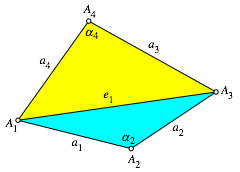
Abb. 1: Unterteilung
Fr den Flcheninhalt A des Viereckes gilt daher:
![]()
Nach dem
Kosinussatz gilt fr die Diagonale ![]() :
:
![]()
Somit haben wir die Nebenbedingung:
![]()
Wir haben
die Funktion ![]() unter der
Nebenbedingung
unter der
Nebenbedingung ![]() zu optimieren.
zu optimieren.
Nach dem blichen Verfahren bilden wir die Hilfsfunktion
![]()
und setzen deren Gradienten null:
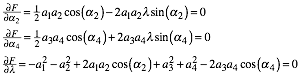
Die ersten beiden Gleichungen lauten vereinfacht:
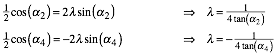
Aus ![]() folgt
folgt ![]() . Wir haben ein Sehnenviereck.
. Wir haben ein Sehnenviereck.
3 Allgemein
Fr den allgemeinen Fall setzen wir die Existenz einer Lsung voraus. Jakob Steiner hat das auch so gemacht.
Nun zeigen wir, dass der Flcheninhalt eines nicht-Sehnen-n-Ecks vergr§ert werden kann.
Dazu
zeichnen wir zunchst den Kreis durch die drei Punkte ![]() (Abb. 2).
Da das n-Eck kein Sehnen-n-Eck ist, gibt es mindestens einen
Punkt
(Abb. 2).
Da das n-Eck kein Sehnen-n-Eck ist, gibt es mindestens einen
Punkt ![]() , der nicht auf diesem Kreis liegt.
, der nicht auf diesem Kreis liegt.
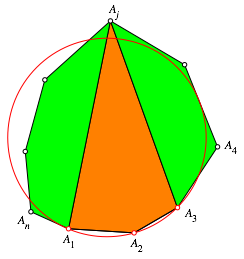
Abb. 2: Beweisfigur
Wir
unterteilen nun das n-Eck in das
Viereck ![]() (orange)
und die beiden Vielecke
(orange)
und die beiden Vielecke ![]() und
und ![]() (grn). Die
beiden grnen Vielecke knnen in Sonderfllen Strecken sein.
(grn). Die
beiden grnen Vielecke knnen in Sonderfllen Strecken sein.
Nun
denken wir uns die beiden grnen Vielecke starr, aber im Punkt ![]() gelenkig
verbunden. Das orange Viereck denken wir uns als Gelenkfigur. Da es kein
Sehnenviereck ist, vergr§ert sich sein Flcheninhalt, wenn wir es unter
Beibehaltung der Seitenlngen in ein Sehnenviereck bewegen.
gelenkig
verbunden. Das orange Viereck denken wir uns als Gelenkfigur. Da es kein
Sehnenviereck ist, vergr§ert sich sein Flcheninhalt, wenn wir es unter
Beibehaltung der Seitenlngen in ein Sehnenviereck bewegen.
Da die grnen Vielecke starr sind, hat sich deren Flcheninhalt nicht verndert. Wegen der Vergr§erung des orangen Vierecks ist der gesamte Flcheninhalt des n-Ecks gr§er geworden.
Somit gilt allgemein, dass der Flcheninhalt genau fr ein Sehnen-n-Eck maximal ist.
4 Bestimmung des optimalen Vielecks. Offene Fragen
4.1 Bestimmung des Sehnenviereckes
Zu gegebenen vier Seiten ist ein Viereck bei Kenntnis eines Winkels bestimmt.
Wenn wir
nun ![]() in die
Nebenbedingung
in die
Nebenbedingung ![]() einsetzen,
erhalten wir:
einsetzen,
erhalten wir:
![]()
Die
Abbildung 3 zeigt das zu den Seitenlngen ![]() des
Viereckes der Abbildung 1 gehrende Sehnenviereck.
des
Viereckes der Abbildung 1 gehrende Sehnenviereck.

Abb. 3: Sehnenviereck
Fr
weitere Berechnungen im Sehnenviereck siehe [Weblink
1].
Fr mich
offene Frage: Gibt es eine direkte einfache Konstruktion?
4.2
Allgemeines Sehnenvieleck
Die
Bestimmung des Sehnen-n-Ecks aus den n Seitenlngen ist fr mich eine offene
Frage, ebenso die direkte Berechnung des Umkreisradius und des Flcheninhaltes.
Weblinks
[Weblink
1]: Flchenoptimierung im Viereck