Hans Walser, [20111120b]

Jedes zweite ist schwarz

Analyse und Spielereien um die Formulierung „jedes zweite“.

Es zeigen sich Paritätsprobleme.

1 Schachbrett

Im Schachbrett (Abb. 1) ist jedes zweite Feld schwarz.

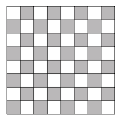
Abb. 1: Schachbrett

Tatsächlich ist es so, dass von zwei unmittelbar benachbarten Feldern das eine weiß und das andere schwarz ist.

Wenn wir jedoch so durchgehen, wie die Christen schreiben, nämlich links oben beginnen und dann zeilenweise von links nach rechts, ergibt sich die Farbverteilung:

wswswswsswswswswwswswsws....

Wir haben nach jedem achten Schritt einen Hiatus. Wenn man den Hiatus vermeiden wollte, sähe das Schachbrett aus wie in Abbildung 2.

Abb. 2: Jedes zweite Feld ist schwarz

Frage 1: Was ist das Geheimnis des Schachbretts der Abbildung 3?

Abb. 3: Und?

1.1 Weiß-schwarz-Wege

Natürlich können wir die Sache retten, indem wir in jeder zweiten Zeile von rechts nach links zählen. Wir haben einen weiß-schwarz-Weg der Länge 63 (Abb. 4). Auf diesem Wege ist jedes zweite durchfahrene Feld schwarz.

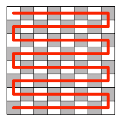
Abb. 4: Weiß-schwarz-Weg

In der Abbildung 5 weitere Beispiele von weiß-schwarz-Wegen. Die Wege dürfen sich nicht überkreuzen.

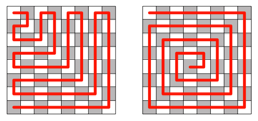
Abb. 5: Weitere Beispiele

Frage 2: Ist es immer so, dass die Wege in einem schwarzen Feld enden?

Es gibt auch geschlossene Wege (Abb. 6). Diese haben die Länge 64. Das Beispiel links hat eine waagerechte Symmetrieachse.

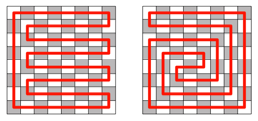
Abb. 6: Geschlossene Wege

In der Abbildung 7 Beispiele mit Symmetrien.

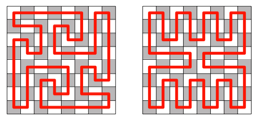
Abb. 7: Symmetrien

Frage 3: Welche Symmetrien haben wir in den Beispielen der Abbildung 7?

Frage 4: Gibt es Wege mit einer Diagonalen des Schachbrettes als Symmetrieachse?

Die Beispiele der Abbildung 8 sind misslungene Versuche, einen geschlossenen Weg mit vierteiliger Drehsymmetrie zu finden. In beiden Fällen sind vier Felder nicht besucht worden (cyan markiert).

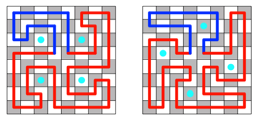
Abb. 8: Vierteilige Drehsymmetrie

Frage 5: Gibt es Wege mit vierteiliger Drehsymmetrie?

2 Statistik und Kombinatorik

Die Redensart „jedes zweite“ wird oft in einem summarischen Sinn verstanden: „die Hälfte“ oder „50%“. Beim regulären Schachbrett sind tatsächlich 32 von 64 Feldern schwarz, also genau die Hälfte.

Frage 6: Wie ist es bei einem (Abb. 9)?

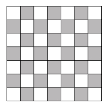
Abb. 9: Sieben mal sieben

Frage 7: Gibt es weiß-schwarz-Wege auf dem ?

Frage 8: Gibt es geschlossene weiß-schwarz-Wege auf dem ?

Frage 9: Wie viele Möglichkeiten gibt es, auf einem 32 Felder schwarz zu färben?

3 Schachbrett im Dreiecksraster

Im dreieckigen Schachbrett der Abbildung 10 ist jedes zweite Feld schwarz.

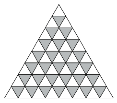
Abb. 10: Schachbrett im Dreiecksraster

Frage 10: Wie groß ist der Anteil der schwarzen Felder?

Frage 11: Allgemein: Wie groß ist der Anteil der schwarzen Felder in einem dreieckigen Schachbrett der Kantenlänge k?

Frage 12: Gibt es weiß-schwarz-Wege in einem dreieckigen Schachbrett?

Aus sechs dreieckigen Schachbrettern lässt sich ein sechseckiges Schachbrett zusammensetzen (Abb. 11).

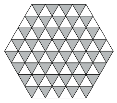
Abb. 11: Sechseckiges Schachbrett

Frage 13: Wie groß in einem sechseckigen Schachbrett ist der Anteil der schwarzen Felder?

Frage 14: Gibt es weiß-schwarz-Wege im sechseckigen Schachbrett?

Frage 15: Gibt es geschlossene weiß-schwarz-Wege im sechseckigen Schachbrett?

4 Beantwortung der Fragen

Frage 1: Was ist das Geheimnis des folgenden Schachbretts? — Das Brett wurde auf eine Spitze gestellt und dann horizontal zeilenweise von links nach rechts weiß-schwarz gefärbt (Abb. 12).

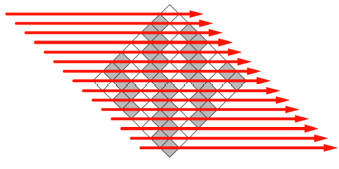
Abb. 12: Brett auf Spitze

Frage 2: Ist es immer so, dass die Wege in einem schwarzen Feld enden? — Ja. Weil jedes zweite Feld schwarz ist, die Wege aber im weißen Feld links oben beginnen und über alle 64 Felder laufen, ist das letzte Feld schwarz.

Frage 3: Welche Symmetrien haben wir in den Beispielen der Abbildung 7? — Beispiel links: Punktsymmetrie. Beispiel rechts: Punktsymmetrie, waagerechte und senkrechte Symmetrieachsen.

Frage 4: Gibt es Wege mit einer Diagonalen des Schachbrettes als Symmetrieachse? — Nein. Situation auf den Diagonalenfeldern studieren.

Frage 5: Gibt es Wege mit vierteiliger Drehsymmetrie?— Nein. Ein Viertelweg hat Anfangs- und Endpunkt in Feldern verschiedener Farben. Dann ist seine Länge ungerade (Abb. 13). Die Länge müsste aber 16 sein.

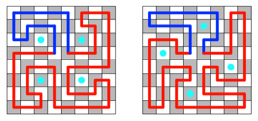
Abb. 13: Viertel falscher Länge

Frage 6: Wie ist es bei einem ? — Wir haben 49 Felder, davon 24 schwarze, also weniger als die Hälfte. Andererseits ist bei einem zeilenweisen horizontalen Durchlauf jedes zweite Feld schwarz (Abb. 14).

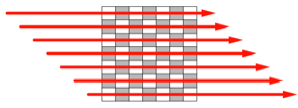
Abb. 14: Jedes zweite Feld ist schwarz

Frage 7: Gibt es weiß-schwarz-Wege auf dem ? — Die Abbildung 15 zeigt drei Beispiele. Anfang und Ende der Wege sind in Feldern gleicher Farbe.

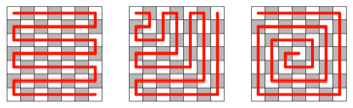
Abb. 15: Wege

Frage 8: Gibt es geschlossene weiß-schwarz-Wege auf dem ? — Nein. Ein geschlossener Weg müsste eine gerade Anzahl Felder treffen. Das hat 49 Felder.

Frage 9: Wie viele Möglichkeiten gibt es, auf einem 32 Felder schwarz zu färben? — Anzahl der Möglichkeiten:

Frage 10: Wie groß ist der Anteil der schwarzen Felder? — Wir haben 28 schwarze Felder und 36 weiße Felder. Der Anteil ist also . Deutlich weniger als die Hälfte.

Frage 11: Wie groß ist der Anteil der schwarzen Felder in einem dreieckigen Schachbrett der Kantenlänge k? — Tabelle:

k	1	2	3	4	5	6	7	8
weiß	1	3	6	10	15	21	28	36
schwarz	0	1	3	6	10	15	21	28
Summe	1	4	9	16	25	36	49	64
Differenz	1	2	3	4	5	6	7	8
Anteil schwarz	0	0.25		0.375	0.4			0.4375

Formeln:

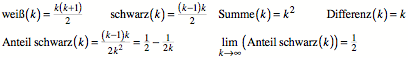
Frage 12: Gibt es weiß-schwarz-Wege in einem dreieckigen Schachbrett? — Nein. Es hat zu viele weiße Felder. Zudem sind die weißen Felder an den Ecken dead ends. Ein Weg müsste dort starten oder enden. Wir haben aber drei solcher weißen Felder.

Frage 13: Wie groß in einem sechseckigen Schachbrett ist der Anteil der schwarzen Felder? — Genau die Hälfte.

Frage 14: Gibt es weiß-schwarz-Wege im sechseckigen Schachbrett? — Ja. Die Abbildung 16 zeigt ein Beispiel. Dieses Beispiel ist aber auch (bis auf Symmetrien) das einzige. Der Grund liegt darin, dass die weiß-schwarz-Wege keine scharfen Kurven fahren können, nur Richtungsänderungen von 60°. Bei Richtungsänderungen von 120° entsteht ein Mauerblümchenfeld, das nicht berührt wird.

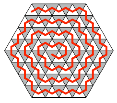
Abb. 16: Weg

Dieses Beispiel ist aber auch (bis auf Symmetrien) das einzige. Der Grund liegt darin, dass die weiß-schwarz-Wege keine scharfen Kurven fahren können, nur Richtungsänderungen von 60°. Bei Richtungsänderungen von 120° bleibt ein Mauerblümchenfeld, das nicht berührt wird. Die Abbildung 17 illustriert den Sachverhalt. Die Mauerblümchen sind cyan markiert.

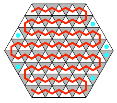
Abb. 17: Mauerblümchen

Frage 15: Gibt es geschlossene weiß-schwarz-Wege im sechseckigen Schachbrett? — Nein. Die einzige Ausnahme ist das minimale Schachbrett (Abb. 18).

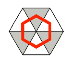
Abb. 18: Geschlossener Weg im Minimalmodell